Trigonometric. Modulus and argument of a complex number. Trigonometric notation How to find an argument
Definition 8.3 (1).
Length |z| vector z = (x,y) is called the modulus of the complex number z = x + yi
Since the length of each side of the triangle does not exceed the sum of the lengths of its two other sides, and the absolute value of the difference in the lengths of the two sides of the triangle is not less than the length of the third side, then for any two complex numbers z 1 and z 2 the inequalities hold

Definition 8.3 (2).
Complex number argument. If φ is the angle formed by a non-zero vector z with the real axis, then any angle of the form (φ + 2πn, where n is an integer, and only an angle of this kind, will also be an angle formed by the vector z with the real axis.
The set of all angles formed by the non-zero vector z = = (x, y) with the real axis is called the argument of the complex number z = x + yi and is denoted by arg z. Each element of this set is called the value of the argument of the number z (Fig. 8.3(1)).
Rice. 8.3(1).
Since a non-zero vector of a plane is uniquely determined by its length and the angle it forms with the x axis, then two complex numbers different from zero are equal if and only if their absolute values and arguments are equal.
If, for example, the condition 0≤φ is imposed on the values of the argument φ of the number z<2π или условие -π<φ≤π, то значение аргумента будет определено однозначно. Такое значение называется главным значением аргумента.
Definition 8.3.(3)
Trigonometric form of writing a complex number. The real and imaginary parts of a complex number z = x + уi ≠ 0 are expressed through its modulus r= |z| and the argument φ as follows (from the definition of sine and cosine):
The right side of this equality is called the trigonometric form of writing the complex number z. We will also use it for z = 0; in this case, r = 0, and φ can take any value - the argument of the number 0 is undefined. So, every complex number can be written in trigonometric form.
It is also clear that if the complex number z is written in the form
then the number r is its modulus, since
And φ is one of the values of its argument
The trigonometric form of writing complex numbers can be convenient to use when multiplying complex numbers; in particular, it allows you to find out the geometric meaning of the product of complex numbers.
Let's find formulas for multiplying and dividing complex numbers in trigonometric form. If
then according to the rule of multiplication of complex numbers (using the formulas for sine and cosine of the sum)
Thus, when multiplying complex numbers, their absolute values are multiplied, and the arguments are added:
Applying this formula sequentially to n complex numbers, we get
If all n numbers are equal, we get
Where for
performed
![]()
Hence, for a complex number whose absolute value is 1 (hence, it has the form
![]()
This equality is called Moivre's formulas
In other words, when dividing complex numbers, their modules are divided,
and the arguments are subtracted.
Examples 8.3 (1).
Draw on the complex plane C a set of points satisfying the following conditions:

Corresponding to this number: .
The modulus of a complex number z is usually denoted | z| or r.
Let and be real numbers such that a complex number (usual notation). Then
Wikimedia Foundation. 2010.
See what “Modulus of a complex number” is in other dictionaries:
modulus of a complex number- kompleksinio skaičiaus modulis statusas T sritis fizika atitikmenys: engl. modulus of complex number vok. Betrag der komplexen Zahl, m rus. modulus of a complex number, m pranc. module du nombre complexe, m … Fizikos terminų žodynas
- (modulus) The magnitude of a number in terms of its distance from 0. The modulus, or absolute value of a real number x (denoted by |x|), is the difference between x and 0, regardless of sign. Therefore, if x0, then |x|=x and if x 0, then |x|=–x... Economic dictionary
For a complex number, see Absolute value. The modulus of transition from a system of logarithms with base a to a system with base b is the number 1/logab... Big Encyclopedic Dictionary
The absolute value or modulus of a real or complex number x is the distance from x to the origin. More precisely: The absolute value of a real number x is a non-negative number, denoted by |x| and defined as follows: ... ... Wikipedia
Module in mathematics, 1) M. (or absolute value) of a complex number z = x + iy is the number ═ (the root is taken with a plus sign). When representing a complex number z in trigonometric form z = r(cos j + i sin j), the real number r is equal to... ...
- (in mathematics) a measure for comparing homogeneous quantities and for expressing one of them using another; m. is expressed as a number. Dictionary of foreign words included in the Russian language. Pavlenkov F., 1907. MODULE (lat.). 1) a number that multiplies... ... Dictionary of foreign words of the Russian language
MODULE of a complex number, see Absolute value (see ABSOLUTE VALUE). The modulus of transition from a system of logarithms with base a to a system with base b is the number 1/logab... encyclopedic Dictionary
I Module (from Latin modulus measure) in architecture, a conventional unit adopted to coordinate the sizes of parts of a building or complex. In the architecture of different peoples, depending on the characteristics of construction technology and the composition of buildings behind M... ... Great Soviet Encyclopedia
I; m. [from lat. modulus measure] 1. of what. Specialist. A quantity characterizing which l. property of a solid. M. compression. M. elasticity. 2. Math. Real number, the absolute value of a negative or positive number. M. complex number. M... encyclopedic Dictionary
Numerical characteristics of any mathematical object. Usually the value of M is a non-negative real number, an element that has certain characteristics. properties determined by the properties of the set of objects under consideration. The concept of M.... ... Mathematical Encyclopedia
A complex number is a number of the form z =x + i * y, where x and y are real numbers, and i = imaginary unit (i.e. a number whose square is -1). To define the concept argument comprehensive numbers, it is necessary to consider a complex number on the complex plane in the polar coordinate system.
Instructions
The plane on which complex complexes are represented numbers, is called complex. On this plane, the horizontal axis is occupied by real numbers(x), and the vertical axis is imaginary numbers(y). On such a plane, the number is given by two coordinates z = (x, y). In the polar coordinate system, the coordinates of a point are the modulus and the argument. The modulus is the distance |z| from a point to the origin. The argument is the angle between the vector connecting the point and the origin and the horizontal axis of the coordinate system (see figure).
The figure shows that the complex module numbers z = x + i * y is found using the Pythagorean theorem: |z| = ? (x^2 + y^2). Next argument numbers z is found as an acute angle of a triangle - through the values of the trigonometric functions sin, cos, tg:sin = y / ? (x^2 + y^2),
cos = x / ? (x^2 + y^2),
tg = y/x.
For example, let the number z = 5 * (1 + ?3 * i) be given. First of all, select the real and imaginary parts: z = 5 +5 * ?3 * i. It turns out that the real part is x = 5, and the imaginary part is y = 5 * ?3. Calculate modulus numbers: |z| = ?(25 + 75) = ?100 =10. Next, find the sine of the angle: sin = 5 / 10 = 1 / 2. This gives the argument numbers z is equal to 30°.
Example 2. Let the number z = 5 * i be given. The figure shows that the angle = 90°. Check this value using the formula given above. Write down the coordinates of this numbers on the complex plane: z = (0, 5). Module numbers|z| = 5. Tangent of the angle tg = 5 / 5 = 1. It follows that = 90°.
Example 3. Let it be necessary to find the argument of the sum of two complex numbers z1 = 2 + 3 * i, z2 = 1 + 6 * i. According to the rules of addition, you add these two complex numbers: z = z1 + z2 = (2 + 1) + (3 + 6) * i = 3 + 9 * i. Next, using the above diagram, calculate the argument: tg = 9 / 3 = 3.
Complex numbers
Imaginary And complex numbers. Abscissa and ordinate
complex number. Conjugate complex numbers.
Operations with complex numbers. Geometric
representation of complex numbers. Complex plane.
Modulus and argument of a complex number. Trigonometric
complex number form. Operations with complex
numbers in trigonometric form. Moivre's formula.
Basic information about imaginary And complex numbers are given in the section “Imaginary and complex numbers”. The need for these numbers of a new type arose when solving quadratic equations for the case
D< 0 (здесь D– discriminant of a quadratic equation). For a long time, these numbers did not find physical application, which is why they were called “imaginary” numbers. However, now they are very widely used in various fields of physics.and technology: electrical engineering, hydro- and aerodynamics, elasticity theory, etc.
Complex numbers are written in the form:a+bi. Here a And b – real numbers , A i – imaginary unit, i.e. e. i 2 = –1. Number a called abscissa, a b – ordinatecomplex numbera + bi.Two complex numbersa+bi And a–bi are called conjugate complex numbers.
Main agreements:
1. Real number
Acan also be written in the formcomplex number:a + 0 i or a – 0 i. For example, records 5 + 0i and 5 – 0 imean the same number 5 .2. Complex number 0 + bicalled purely imaginary number. Recordbimeans the same as 0 + bi.
3. Two complex numbersa+bi Andc + diare considered equal ifa = c And b = d. Otherwise complex numbers are not equal.
Addition. Sum of complex numbersa+bi And c + diis called a complex number (a+c ) + (b+d ) i.Thus, when adding complex numbers, their abscissas and ordinates are added separately.
This definition corresponds to the rules for operations with ordinary polynomials.
Subtraction. The difference of two complex numbersa+bi(diminished) and c + di(subtrahend) is called a complex number (a–c ) + (b–d ) i.
Thus, When subtracting two complex numbers, their abscissas and ordinates are subtracted separately.
Multiplication. Product of complex numbersa+bi And c + di is called a complex number:
(ac–bd ) + (ad+bc ) i.This definition follows from two requirements:
1) numbers a+bi And c + dimust be multiplied like algebraic binomials,
2) number ihas the main property:i 2 = – 1.
EXAMPLE ( a+ bi )(a–bi) =a 2 + b 2 . Hence, work
two conjugate complex numbers is equal to the real
a positive number.
Division. Divide a complex numbera+bi (divisible) by anotherc + di(divider) - means to find the third numbere + f i(chat), which when multiplied by a divisorc + di, results in the dividenda + bi.
If the divisor is not zero, division is always possible.
EXAMPLE Find (8 +i ) : (2 – 3 i) .
Solution. Let's rewrite this ratio as a fraction:
Multiplying its numerator and denominator by 2 + 3i
AND Having performed all the transformations, we get:

Geometric representation of complex numbers. Real numbers are represented by points on the number line:
Here is the point Ameans the number –3, dotB– number 2, and O- zero. In contrast, complex numbers are represented by points on the coordinate plane. For this purpose, we choose rectangular (Cartesian) coordinates with the same scales on both axes. Then the complex numbera+bi will be represented by a dot P with abscissa a and ordinate b (see picture). This coordinate system is called complex plane .
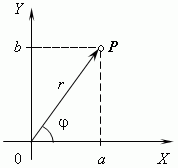
Module complex number is the length of the vectorOP, representing a complex number on the coordinate ( comprehensive) plane. Modulus of a complex numbera+bi denoted | a+bi| or letter r
A complex number is a number of the form z =x + i * y, where x and y are real numbers, and i = imaginary unit (i.e. a number whose square is -1). To define the representation argument comprehensive numbers, you need to look at a complex number on the complex plane in the polar coordinate system.
Instructions
1. The plane on which complex complexes are represented numbers, is called complex. On this plane, the horizontal axis is occupied by real numbers(x), and the vertical axis is imaginary numbers(y). On such a plane, the number is given by two coordinates z = (x, y). In the polar coordinate system, the coordinates of a point are the modulus and the argument. The modulus is the distance |z| from a point to the origin. Is an angle called an argument? between the vector connecting the point and the coordinate preface and the horizontal axis of the coordinate system (see figure).
2. The figure shows that the complex module numbers z = x + i * y is found using the Pythagorean theorem: |z| = ? (x^2 + y^2). Further argument numbers z is found as an acute angle of a triangle - through the values of the trigonometric functions sin, cos, tan:sin? =y/? (x^2 + y^2),cos ? = x / ? (x^2 + y^2),tg ? = y/x.
3. Let's say, let the number z = 5 * (1 + ?3 * i) be given. First of all, select the real and imaginary parts: z = 5 +5 * ?3 * i. It turns out that the real part is x = 5, and the imaginary part is y = 5 * ?3. Calculate modulus numbers: |z| = ?(25 + 75) = ?100 =10. Next, find the sine of the angle?: sin ? = 5 / 10 = 1 / 2. From there we get the argument numbers z is equal to 30°.
4. Example 2. Let the number z = 5 * i be given. From the picture you can see that the angle? = 90°. Check this value using the formula given above. Write down the coordinates of this numbers on the complex plane: z = (0, 5). Module numbers|z| = 5. Tangent of the angle tg? = 5 / 5 = 1. From there it follows what? = 90°.
5. Example 3. Let's say we need to find the argument for the sum of 2 complex numbers z1 = 2 + 3 * i, z2 = 1 + 6 * i. According to the rules of addition, you add these two complex numbers: z = z1 + z2 = (2 + 1) + (3 + 6) * i = 3 + 9 * i. Then, according to the above diagram, calculate the argument: tg? = 9 / 3 = 3.
Note!
If the number z = 0, then the value of the argument for it is not defined.
Helpful advice
The value of the argument of a complex number is determined with an accuracy of 2 * ? * k, where k is any integer. The meaning of the argument? such that –?
What else to read
THE LAST NOTES
- Liquid buckwheat porridge - benefits in every spoon
- Step-by-step photo recipe for freezing vegetables for borscht for the winter at home Freezing borscht for the winter with beets
- Information support for small businesses Types of state support for small businesses
- Snow Maiden Russian folk tale
- Causes of the Thirty Years' War
