Probability of a normally distributed random variable. Normal probability distribution law for a continuous random variable. Relationship with other distributions
Substituting φ(x)=π /4 ,f(x)=1/(b-a)
D[π /4]=( /720) ).
№319 cube edge x measured approximately, and a . Considering the edge of a cube as a random variable X, distributed uniformly in the interval (a, b), find the mathematical expectation and variance of the volume of the cube.
1. Let’s find the mathematical expectation of the area of a circle – a random variable Y=φ(K)= - according to the formula
M[φ(X)]= ![]()
By placing φ(x)= ,f(x)=1/(b-a) and performing integration, we get
M( )=
 .
.
2. Find the dispersion of the area of a circle using the formula
D [φ(X)]= ![]() -
-
![]() .
.
Substituting φ(x)= ,f(x)=1/(b-a) and performing integration, we get
D =
 .
.
№320 Random variables X and Y are independent and distributed uniformly: X in the interval (a, b), Y in the interval (c, d). Find the mathematical expectation of the product XY.
The mathematical expectation of the product of independent random variables is equal to the product of their mathematical expectations, i.e.
M(XY)= 
№321 Random variables X and Y are independent and distributed uniformly: X in the interval (a,b), Y in the interval (c,d). Find the variance of the product XY.
Let's use the formula
D(XY)=M[
The mathematical expectation of the product of independent random variables is equal to the product of their mathematical expectations, therefore
Let's find M using the formula
M[φ(X)]= ![]()
Substituting φ(x)= ,f(x)=1/(b-a) and performing integration, we get
M (**)
We can similarly find
M (***)
Substituting M(X)=(a+b)/2, M(Y)=(c+d)/2, as well as (***) and (**) in (*), we finally get
D(XY)= -[
![]() .
.
№322 The mathematical expectation of a normally distributed random variable X is a=3 and the standard deviation σ=2. Write the probability density of X.
Let's use the formula:
f(x)=  .
.
Substituting the available values we get:
f(x)=  =f(x)=
=f(x)=  .
.
№323 Write the probability density of a normally distributed random variable X, knowing that M(X)=3, D(X)=16.
Let's use the formula:
f(x)=  .
.
In order to find the value of σ, we use the property that the standard deviation of a random variable X equal to the square root of its variance. Therefore σ=4, M(X)=a=3. Substituting into the formula we get
f(x)=  =
=
 .
.
№324 A normally distributed random variable X is given by density
f(x)= ![]() .
Find the mathematical expectation and variance of X.
.
Find the mathematical expectation and variance of X.
Let's use the formula
f(x)=  ,
,
Where a-expected value, σ - standard deviation X. From this formula it follows that a=M(X)=1. To find the variance, we use the property that the standard deviation of a random variable X equal to the square root of its variance. Hence D(X)= =
Answer: mathematical expectation is 1; the variance is 25.
Bondarchuk Rodion
Given the distribution function of the normalized normal law ![]() . Find the distribution density f(x).
. Find the distribution density f(x).
Knowing that ![]() , find f(x).
, find f(x).

Answer: ![]()
Prove that the Laplace function ![]() . odd:
. odd: ![]() .
.

We will make a replacement


We do the reverse substitution and get:
![]() =
= ![]() =
=


There will also be problems for you to solve on your own, to which you can see the answers.
Normal distribution: theoretical foundations
Examples of random variables distributed according to a normal law are the height of a person and the mass of fish of the same species caught. Normal distribution means the following : there are values of human height, the mass of fish of the same species, which are intuitively perceived as “normal” (and in fact, averaged), and in a sufficiently large sample they are found much more often than those that differ upward or downward.
The normal probability distribution of a continuous random variable (sometimes a Gaussian distribution) can be called bell-shaped due to the fact that the density function of this distribution, symmetric about the mean, is very similar to the cut of a bell (red curve in the figure above).
The probability of encountering certain values in a sample is equal to the area of the figure under the curve, and in the case of a normal distribution we see that under the top of the “bell”, which corresponds to values tending to the average, the area, and therefore the probability, is greater than under the edges. Thus, we get the same thing that has already been said: the probability of meeting a person of “normal” height and catching a fish of “normal” weight is higher than for values that differ upward or downward. In many practical cases, measurement errors are distributed according to a law close to normal.
Let's look again at the figure at the beginning of the lesson, which shows the density function of a normal distribution. The graph of this function was obtained by calculating a certain data sample in the software package STATISTICA. On it, the histogram columns represent intervals of sample values, the distribution of which is close to (or, as is commonly said in statistics, does not differ significantly from) the actual graph of the normal distribution density function, which is a red curve. The graph shows that this curve is indeed bell-shaped.
The normal distribution is valuable in many ways because knowing only the expected value of a continuous random variable and its standard deviation, you can calculate any probability associated with that variable.
The normal distribution also has the advantage of being one of the easiest to use. statistical tests used to test statistical hypotheses - Student's t test- can only be used if the sample data obeys the normal distribution law.
Density function of the normal distribution of a continuous random variable can be found using the formula:
 ,
,
Where x- value of the changing quantity, - average value, - standard deviation, e=2.71828... - the base of the natural logarithm, =3.1416...
Properties of the normal distribution density function
Changes in the mean move the normal density function curve toward the axis Ox. If it increases, the curve moves to the right, if it decreases, then to the left.
If the standard deviation changes, the height of the top of the curve changes. When the standard deviation increases, the top of the curve is higher, and when it decreases, it is lower.
Probability of a normally distributed random variable falling within a given interval
Already in this paragraph we will begin to solve practical problems, the meaning of which is indicated in the title. Let's look at what possibilities theory provides for solving problems. The starting concept for calculating the probability of a normally distributed random variable falling into a given interval is the cumulative function of the normal distribution.
Cumulative normal distribution function:
 .
.
However, it is problematic to obtain tables for every possible combination of mean and standard deviation. Therefore, one of the simple ways to calculate the probability of a normally distributed random variable falling into a given interval is to use probability tables for the standardized normal distribution.
A normal distribution is called standardized or normalized., the mean of which is , and the standard deviation is .
Standardized Normal Distribution Density Function:
![]() .
.
Cumulative function of the standardized normal distribution:
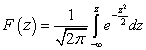 .
.
The figure below shows the integral function of the standardized normal distribution, the graph of which was obtained by calculating a certain data sample in the software package STATISTICA. The graph itself is a red curve, and the sample values are approaching it.

To enlarge the picture, you can click on it with the left mouse button.
Standardizing a random variable means moving from the original units used in the task to standardized units. Standardization is performed according to the formula
In practice, all possible values of a random variable are often unknown, so the values of the mean and standard deviation cannot be determined accurately. They are replaced by the arithmetic mean of observations and standard deviation s. Magnitude z expresses the deviations of the values of a random variable from the arithmetic mean when measuring standard deviations.
Open interval
The probability table for the standardized normal distribution, which can be found in almost any book on statistics, contains the probabilities that a random variable having a standard normal distribution Z will take a value less than a certain number z. That is, it will fall into the open interval from minus infinity to z. For example, the probability that the quantity Z less than 1.5, equal to 0.93319.
Example 1. The company produces parts whose service life is normally distributed with a mean of 1000 hours and a standard deviation of 200 hours.
For a randomly selected part, calculate the probability that its service life will be at least 900 hours.
Solution. Let's introduce the first notation:
The desired probability.
The random variable values are in an open interval. But we know how to calculate the probability that a random variable will take a value less than a given one, and according to the conditions of the problem, we need to find one equal to or greater than a given one. This is the other part of the space under the normal density curve (bell). Therefore, to find the desired probability, you need to subtract from unity the mentioned probability that the random variable will take a value less than the specified 900:
Now the random variable needs to be standardized.
We continue to introduce the notation:
z = (X ≤ 900) ;
x= 900 - specified value of the random variable;
μ = 1000 - average value;
σ = 200 - standard deviation.
Using these data, we obtain the conditions of the problem:
![]() .
.
According to tables of standardized random variable (interval boundary) z= −0.5 corresponds to a probability of 0.30854. Subtract it from unity and get what is required in the problem statement:
So, the probability that the part will have a service life of at least 900 hours is 69%.
This probability can be obtained using the MS Excel function NORM.DIST (integral value - 1):
P(X≥900) = 1 - P(X≤900) = 1 - NORM.DIST(900; 1000; 200; 1) = 1 - 0.3085 = 0.6915.
About calculations in MS Excel - in one of the subsequent paragraphs of this lesson.
Example 2. In a certain city, the average annual family income is a normally distributed random variable with a mean of 300,000 and a standard deviation of 50,000. It is known that the income of 40% of families is less than A. Find the value A.
Solution. In this problem, 40% is nothing more than the probability that the random variable will take a value from an open interval that is less than a certain value, indicated by the letter A.
To find the value A, first we compose the integral function:
![]()
According to the conditions of the problem
μ = 300000 - average value;
σ = 50000 - standard deviation;
x = A- the quantity to be found.
Making up an equality
![]() .
.
From the statistical tables we find that the probability of 0.40 corresponds to the value of the interval boundary z = −0,25 .
Therefore, we create the equality
![]()
and find its solution:
A = 287300 .
Answer: 40% of families have incomes less than 287,300.
Closed interval
In many problems it is required to find the probability that a normally distributed random variable will take a value in the interval from z 1 to z 2. That is, it will fall into a closed interval. To solve such problems, it is necessary to find in the table the probabilities corresponding to the boundaries of the interval, and then find the difference between these probabilities. This requires subtracting the smaller value from the larger one. Examples of solutions to these common problems are the following, and you are asked to solve them yourself, and then you can see the correct solutions and answers.
Example 3. The profit of an enterprise for a certain period is a random variable subject to the normal distribution law with an average value of 0.5 million. and standard deviation 0.354. Determine, to within two decimal places, the probability that the enterprise’s profit will be from 0.4 to 0.6 c.u.
Example 4. The length of the manufactured part is a random variable distributed according to the normal law with parameters μ =10 and σ =0.071. Find the probability of defects, accurate to two decimal places, if the permissible dimensions of the part must be 10±0.05.
Hint: in this problem, in addition to finding the probability of a random variable falling into a closed interval (the probability of receiving a non-defective part), you need to perform one more action.

allows you to determine the probability that the standardized value Z not less -z and no more +z, Where z- an arbitrarily selected value of a standardized random variable.
An approximate method for checking the normality of a distribution
An approximate method for checking the normality of the distribution of sample values is based on the following property of normal distribution: skewness coefficient β 1 and kurtosis coefficient β 2 are equal to zero.
Asymmetry coefficient β 1 numerically characterizes the symmetry of the empirical distribution relative to the mean. If the skewness coefficient is zero, then the arithmetric mean, median and mode are equal: and the distribution density curve is symmetrical about the mean. If the asymmetry coefficient is less than zero (β 1 < 0 ), then the arithmetic mean is less than the median, and the median, in turn, is less than mode () and the curve is shifted to the right (compared to the normal distribution). If the asymmetry coefficient is greater than zero (β 1 > 0 ), then the arithmetic mean is greater than the median, and the median, in turn, is greater than the mode () and the curve is shifted to the left (compared to the normal distribution).
Kurtosis coefficient β 2 characterizes the concentration of the empirical distribution around the arithmetic mean in the direction of the axis Oy and the degree of peaking of the distribution density curve. If the kurtosis coefficient is greater than zero, then the curve is more elongated (compared to the normal distribution) along the axis Oy(the graph is more peaked). If the kurtosis coefficient is less than zero, then the curve is more flattened (compared to the normal distribution) along the axis Oy(the graph is more obtuse).
The asymmetry coefficient can be calculated using the MS Excel SKOS function. If you are checking one data array, then you need to enter the data range in one “Number” box.

The kurtosis coefficient can be calculated using the MS Excel KURTESS function. When checking one data array, it is also sufficient to enter the data range in one “Number” box.

So, as we already know, with a normal distribution the coefficients of skewness and kurtosis are equal to zero. But what if we got skewness coefficients of -0.14, 0.22, 0.43 and kurtosis coefficients of 0.17, -0.31, 0.55? The question is quite fair, since in practice we are dealing only with approximate, sample values of asymmetry and kurtosis, which are subject to some inevitable, uncontrolled scatter. Therefore, one cannot demand that these coefficients be strictly equal to zero; they must only be sufficiently close to zero. But what does enough mean?
It is required to compare the obtained empirical values with acceptable values. To do this, you need to check the following inequalities (compare the values of the modulus coefficients with the critical values - the boundaries of the hypothesis testing area).
For the asymmetry coefficient β 1 .
The normal distribution law is most often encountered in practice. The main feature that distinguishes it from other laws is that it is a limiting law, to which other laws of distribution approach under very common typical conditions.
Definition. A continuous random variable X has normal law distribution(Gauss's law )with parameters a and σ 2 if its probability density f(x) looks like:
| . | (6.19) |
The normal distribution curve is called normal or Gaussian curve. In Fig. 6.5 a), b) shows a normal curve with parameters A And σ 2 and distribution function graph.
 Let us pay attention to the fact that the normal curve is symmetrical with respect to the straight line X = A, has a maximum at the point X = A, equal to , and two inflection points X = A σ
with ordinates.
Let us pay attention to the fact that the normal curve is symmetrical with respect to the straight line X = A, has a maximum at the point X = A, equal to , and two inflection points X = A σ
with ordinates.
It can be noted that in the normal law density expression, the distribution parameters are indicated by the letters A And σ 2, which we used to denote the mathematical expectation and dispersion. This coincidence is not accidental. Let us consider a theorem that establishes the probabilistic theoretical meaning of the parameters of the normal law.
Theorem. The mathematical expectation of a random variable X, distributed according to a normal law, is equal to the parameter a of this distribution, i.e.
| M(X) = A, | (6.20) |
and its dispersion – to the parameter σ 2, i.e.
| D(X) = σ 2. | (6.21) |
Let's find out how the normal curve will change when the parameters change A And σ .
If σ = const, and the parameter changes a (A 1 < A 2 < A 3), i.e. the center of symmetry of the distribution, then the normal curve will shift along the abscissa axis without changing its shape (Fig. 6.6).

Rice. 6.6

Rice. 6.7
If A= const and the parameter changes σ , then the ordinate of the curve maximum changes f max(a) = . When increasing σ the ordinate of the maximum decreases, but since the area under any distribution curve must remain equal to unity, the curve becomes flatter, stretching along the x-axis. When decreasing σ On the contrary, the normal curve extends upward while simultaneously compressing from the sides (Fig. 6.7).
So the parameter a characterizes the position, and the parameter σ – the shape of a normal curve.
Normal distribution law of a random variable with parameters a= 0 and σ = 1 is called standard or normalized, and the corresponding normal curve is standard or normalized.
The difficulty of directly finding the distribution function of a random variable distributed according to the normal law is due to the fact that the integral of the normal distribution function is not expressed through elementary functions. However, it can be calculated through a special function expressing a definite integral of the expression or. This function is called Laplace function, tables have been compiled for it. There are many varieties of this function, for example:
![]() ,
, ![]() .
.
We will use the function
Let us consider the properties of a random variable distributed according to a normal law.
1. The probability of a random variable X, distributed according to a normal law, falling into the interval [α , β ] equal to
Using this formula, we calculate the probabilities for various values δ (using the table of Laplace function values):
at δ = σ = 2Ф(1) = 0.6827;
at δ = 2σ = 2Ф(2) = 0.9545;
at δ = 3σ = 2Ф(3) = 0.9973.
This leads to the so-called “ three sigma rule»:
If a random variable X has a normal distribution law with parameters a and σ, then it is almost certain that its values lie in the interval(a – 3σ ; a + 3σ ).
Example 6.3. Assuming that the height of men of a certain age group is a normally distributed random variable X with parameters A= 173 and σ 2 = 36, find:
1. Expression of probability density and distribution function of a random variable X;
2. The share of suits of the 4th height (176 - 183 cm) and the share of suits of the 3rd height (170 - 176 cm), which must be included in the total production volume for this age group;
3. Formulate the “three sigma rule” for a random variable X.
1. Finding the probability density
![]()
and the distribution function of the random variable X
![]() = .
= .
2. We find the proportion of suits of height 4 (176 – 182 cm) as a probability
R(176 ≤ X ≤ 182) = ![]() = Ф(1.5) – Ф(0.5).
= Ф(1.5) – Ф(0.5).
According to the table of values of the Laplace function ( Appendix 2) we find:
F(1.5) = 0.4332, F(0.5) = 0.1915.
Finally we get
R(176 ≤ X ≤ 182) = 0,4332 – 0,1915 = 0,2417.
The share of suits of the 3rd height (170 – 176 cm) can be found in a similar way. However, it is easier to do this if we take into account that this interval is symmetrical with respect to the mathematical expectation A= 173, i.e. inequality 170 ≤ X≤ 176 is equivalent to inequality │ X– 173│≤ 3. Then
R(170 ≤X ≤176) = R(│X– 173│≤ 3) = 2Ф(3/6) = 2Ф(0.5) = 2·0.1915 = 0.3830.
3. Let us formulate the “three sigma rule” for the random variable X:
It is almost certain that the height of men in this age group ranges from A – 3σ = 173 – 3 6 = 155 to A + 3σ = 173 + 3·6 = 191, i.e. 155 ≤ X ≤ 191. ◄
7. LIMIT THEOREMS OF PROBABILITY THEORY
As already mentioned when studying random variables, it is impossible to predict in advance what value a random variable will take as a result of a single test - it depends on many reasons that cannot be taken into account.
However, when tests are repeated many times, the behavior of the sum of random variables almost loses its random character and becomes natural. The presence of patterns is associated precisely with the mass nature of phenomena that in their totality generate a random variable that is subject to a well-defined law. The essence of the stability of mass phenomena comes down to the following: the specific features of each individual random phenomenon have almost no effect on the average result of the mass of such phenomena; random deviations from the average, inevitable in each individual phenomenon, are mutually canceled out, leveled out, leveled out in the mass.
It is this stability of averages that represents the physical content of the “law of large numbers,” understood in the broad sense of the word: with a very large number of random phenomena, their result practically ceases to be random and can be predicted with a high degree of certainty.
In the narrow sense of the word, the “law of large numbers” in probability theory is understood as a series of mathematical theorems, each of which, for certain conditions, establishes the fact that the average characteristics of a large number of experiments approach certain certain constants.
The law of large numbers plays an important role in the practical applications of probability theory. The property of random variables, under certain conditions, to behave practically like non-random ones allows one to confidently operate with these quantities and predict the results of mass random phenomena with almost complete certainty.
The possibilities of such predictions in the field of mass random phenomena are further expanded by the presence of another group of limit theorems, which concern not the limiting values of random variables, but the limiting laws of distribution. We are talking about a group of theorems known as the “central limit theorem.” The various forms of the central limit theorem differ from each other in the conditions for which this limiting property of the sum of random variables is established.
Various forms of the law of large numbers with various forms of the central limit theorem form a set of so-called limit theorems probability theory. Limit theorems make it possible not only to make scientific forecasts in the field of random phenomena, but also to evaluate the accuracy of these forecasts.
The random variable is called distributed according to the normal (Gaussian) law with parameters A And () , if the probability distribution density has the form
A normally distributed quantity always has an infinite number of possible values, so it is convenient to depict it graphically using a distribution density graph. According to the formula
the probability that a random variable will take a value from an interval is equal to the area under the graph of a function on this interval (the geometric meaning of a definite integral). The function under consideration is non-negative and continuous. The graph of the function has the shape of a bell and is called a Gaussian curve or normal curve.
The figure shows several distribution density curves of a random variable specified according to the normal law.
All curves have one maximum point, and as you move away from it to the right and left, the curves decrease. The maximum is achieved at and is equal to .
The curves are symmetrical about a vertical line drawn through the highest point. The area of the subgraph of each curve is 1.
The difference between individual distribution curves is only that the total area of the subgraph, the same for all curves, is distributed differently between different sections. The main part of the subgraph area of any curve is concentrated in the immediate vicinity of the most probable value, and this value is different for all three curves. For different values and A different normal laws and different density distribution function graphs are obtained.
Theoretical studies have shown that most random variables encountered in practice have a normal distribution law. According to this law, the speed of gas molecules, the weight of newborns, the size of clothes and shoes of the country's population, and many other random events of a physical and biological nature are distributed. This pattern was first noticed and theoretically substantiated by A. Moivre.
For , the function coincides with the function that was already discussed in the local limit theorem of Moivre–Laplace. The probability density of a normal distribution is easy expressed through:
For such parameter values, the normal law is called main .
The distribution function for normalized density is called Laplace function and is designated Φ(x). We have also already encountered this function.
The Laplace function does not depend on specific parameters A and σ. For the Laplace function, using approximate integration methods, tables of values on the interval with varying degrees of accuracy have been compiled. Obviously, the Laplace function is odd, therefore, there is no need to put its values in the table for negative .
For a random variable distributed according to the normal law with parameters A and , mathematical expectation and dispersion are calculated using the formulas: , .The standard deviation is equal to .
The probability that a normally distributed quantity will take a value from the interval is equal to
where is the Laplace function introduced in the integral limit theorem.
Often in problems it is required to calculate the probability that the deviation of a normally distributed random variable X from its mathematical expectation in absolute value does not exceed a certain value, i.e. calculate probability. Applying formula (19.2), we have:
In conclusion, we present one important corollary from formula (19.3). Let's put in this formula . Then, i.e. the probability that the absolute value of the deviation X of its mathematical expectation will not exceed , equal to 99.73%. In practice, such an event can be considered reliable. This is the essence of the three sigma rule.
Three sigma rule. If a random variable is distributed normally, then the absolute value of its deviation from the mathematical expectation practically does not exceed three times the standard deviation.
The article shows in detail what the normal distribution law of a random variable is and how to use it when solving practical problems.
Normal distribution in statistics
The history of the law goes back 300 years. The first discoverer was Abraham de Moivre, who came up with the approximation back in 1733. Many years later, Carl Friedrich Gauss (1809) and Pierre-Simon Laplace (1812) derived mathematical functions.
Laplace also discovered a remarkable pattern and formulated central limit theorem (CPT), according to which the sum of a large number of small and independent quantities has a normal distribution.
The normal law is not a fixed equation of the dependence of one variable on another. Only the nature of this dependence is recorded. The specific form of distribution is specified by special parameters. For example, y = ax + b is the equation of a straight line. However, where exactly it passes and at what angle is determined by the parameters A And b. Same with normal distribution. It is clear that this is a function that describes the tendency of a high concentration of values around the center, but its exact shape is determined by special parameters.
The Gaussian normal distribution curve looks like this.
The normal distribution graph resembles a bell, which is why you might see the name bell curve. The graph has a “hump” in the middle and a sharp decrease in density at the edges. This is the essence of the normal distribution. The probability that a random variable will be near the center is much higher than that it will deviate greatly from the center.

The figure above shows two areas under the Gaussian curve: blue and green. Reasons, i.e. The intervals are equal for both sections. But the heights are noticeably different. The blue area is farther from the center and has a significantly lower height than the green area, which is located in the very center of the distribution. Consequently, the areas, that is, the probabilities of falling into the designated intervals, also differ.
The formula for normal distribution (density) is as follows.
![]()
The formula consists of two mathematical constants:
π – pi number 3.142;
e– natural logarithm base 2.718;
two changeable parameters that define the shape of a specific curve:
m– mathematical expectation (other notations may be used in various sources, for example, µ or a);
σ 2– dispersion;
and the variable itself x, for which the probability density is calculated.
The specific form of the normal distribution depends on 2 parameters: ( m) And ( σ 2). Briefly indicated N(m, σ 2) or N(m, σ). Parameter m(expectation) determines the center of the distribution, which corresponds to the maximum height of the graph. Dispersion σ 2 characterizes the scope of variation, that is, the “smeariness” of the data.
The mathematical expectation parameter shifts the center of the distribution to the right or left without affecting the shape of the density curve itself.

But dispersion determines the sharpness of the curve. When the data has a small scatter, then all its mass is concentrated at the center. If the data has a large scatter, then it is “spread out” over a wide range.

Distribution density has no direct practical application. To calculate the probabilities, you need to integrate the density function.
The probability that a random variable will be less than a certain value x, is determined normal distribution function:
Using the mathematical properties of any continuous distribution, it is easy to calculate any other probabilities, since
P(a ≤ X< b) = Ф(b) – Ф(a)
Standard normal distribution
The normal distribution depends on the parameters of the mean and variance, which is why its properties are poorly visible. It would be nice to have some distribution standard that does not depend on the scale of the data. And it exists. Called standard normal distribution. In fact, this is an ordinary normal distribution, only with the parameters mathematical expectation 0 and variance 1, briefly written N(0, 1).
Any normal distribution can easily be converted into a standard distribution by normalization:
Where z– a new variable that is used instead x;
m- expected value;
σ
- standard deviation.
For sample data, estimates are taken:
Arithmetic mean and variance of the new variable z are now also 0 and 1 respectively. This can be easily verified using elementary algebraic transformations.
The name appears in the literature z-score. This is it – normalized data. Z-score can be directly compared with theoretical probabilities, because its scale coincides with the standard.
Let's now see what the density of the standard normal distribution looks like (for z-scores). Let me remind you that the Gaussian function has the form:
![]()
Let's substitute instead (x-m)/σ letter z, and instead σ – one, we get density function of the standard normal distribution:
![]()
Density chart:

The center, as expected, is at point 0. At the same point, the Gaussian function reaches its maximum, which corresponds to the random variable accepting its average value (i.e. x-m=0). The density at this point is 0.3989, which can be calculated even in your head, because e 0 =1 and all that remains is to calculate the ratio of 1 to the root of 2 pi.
Thus, the graph clearly shows that values that have small deviations from the average occur more often than others, and those that are very far from the center occur much less frequently. The x-axis scale is measured in standard deviations, which allows you to get rid of units of measurement and obtain a universal structure of a normal distribution. The Gaussian curve for normalized data perfectly demonstrates other properties of the normal distribution. For example, that it is symmetrical about the ordinate axis. Most of all values are concentrated within ±1σ from the arithmetic mean (we estimate by eye for now). Most of the data are within ±2σ. Almost all data are within ±3σ. The last property is widely known as three sigma rule for normal distribution.
The standard normal distribution function allows you to calculate probabilities.
![]()
It’s clear that no one counts manually. Everything is calculated and placed in special tables, which are at the end of any statistics textbook.
Normal distribution table
There are two types of normal distribution tables:
- table density;
- table functions(integral of density).
Table density rarely used. However, let's see how it looks. Let's say we need to get the density for z = 1, i.e. density of a value separated from the expectation by 1 sigma. Below is a piece of the table.

Depending on the organization of the data, we look for the desired value by the name of the column and row. In our example we take the line 1,0 and column 0 , because there are no hundredths. The value you are looking for is 0.2420 (the 0 before 2420 is omitted).
The Gaussian function is symmetrical about the ordinate. That's why φ(z)= φ(-z), i.e. density for 1 is identical to the density for -1 , which is clearly visible in the figure.

To avoid wasting paper, tables are printed only for positive values.
In practice, the values are more often used functions standard normal distribution, that is, the probability for different z.
Such tables also contain only positive values. Therefore, to understand and find any you should know the required probabilities properties of the standard normal distribution.
Function Ф(z) symmetrical about its value 0.5 (and not the ordinate axis, like density). Hence the equality is true:
This fact is shown in the picture:

Function values Ф(-z) And Ф(z) divide the graph into 3 parts. Moreover, the upper and lower parts are equal (indicated by check marks). To complement the probability Ф(z) to 1, just add the missing value Ф(-z). You get the equality indicated just above.
If you need to find the probability of falling into the interval (0; z), that is, the probability of deviation from zero in a positive direction to a certain number of standard deviations, it is enough to subtract 0.5 from the value of the standard normal distribution function:

For clarity, you can look at the drawing.

On a Gaussian curve, this same situation looks like the area from center right to z.

Quite often, an analyst is interested in the probability of deviation in both directions from zero. And since the function is symmetrical about the center, the previous formula must be multiplied by 2:

Picture below.

Under the Gaussian curve this is the central part limited by the selected value –z left and z on right.

These properties should be taken into account, because tabulated values rarely correspond to the interval of interest.
To make the task easier, textbooks usually publish tables for functions of the form:

If you need the probability of deviation in both directions from zero, then, as we have just seen, the table value for this function is simply multiplied by 2.
Now let's look at specific examples. Below is a table of the standard normal distribution. Let's find the table values for three z: 1.64, 1.96 and 3.

How to understand the meaning of these numbers? Let's start with z=1.64, for which the table value is 0,4495 . The easiest way to explain the meaning is in the figure.

That is, the probability that a standardized normally distributed random variable falls within the interval from 0 before 1,64 , is equal 0,4495 . When solving problems, you usually need to calculate the probability of deviation in both directions, so let’s multiply the value 0,4495 by 2 and we get approximately 0.9. The occupied area under the Gaussian curve is shown below.

Thus, 90% of all normally distributed values fall within the interval ±1.64σ from the arithmetic mean. It was not by chance that I chose the meaning z=1.64, because the neighborhood around the arithmetic mean, occupying 90% of the entire area, is sometimes used to calculate confidence intervals. If the value being tested does not fall within the designated area, then its occurrence is unlikely (only 10%).
To test hypotheses, however, an interval covering 95% of all values is more often used. Half the chance 0,95 - This 0,4750 (see the second highlighted value in the table).

For this probability z=1.96. Those. within almost ±2σ 95% of values are from the average. Only 5% fall outside these limits.

Another interesting and frequently used table value corresponds to z=3, it is equal according to our table 0,4986 . Multiply by 2 and get 0,997 . So, within ±3σ Almost all values are derived from the arithmetic mean.

This is what the 3 sigma rule looks like for a normal distribution in a diagram.
Using statistical tables you can get any probability. However, this method is very slow, inconvenient and very outdated. Today everything is done on the computer. Next, we move on to the practice of calculations in Excel.
Normal Distribution in Excel
Excel has several functions for calculating probabilities or inverses of a normal distribution.

NORMAL DIST function
Function NORM.ST.DIST. designed to calculate density ϕ(z) or probabilities Φ(z) according to normalized data ( z).
=NORM.ST.DIST(z;integral)
z– value of the standardized variable
integral– if 0, then the density is calculatedϕ(z) , if 1 is the value of the function Ф(z), i.e. probability P(Z
Let's calculate the density and function value for various z: -3, -2, -1, 0, 1, 2, 3(we will indicate them in cell A2).
To calculate the density, you will need the formula =NORM.ST.DIST(A2;0). In the diagram below, this is the red dot.
To calculate the value of the function =NORM.ST.DIST(A2;1). The diagram shows the shaded area under the normal curve.

In reality, it is more often necessary to calculate the probability that a random variable will not go beyond certain limits from the average (in standard deviations corresponding to the variable z), i.e. P(|Z|

Let us determine the probability of a random variable falling within the limits ±1z, ±2z and ±3z from zero. Need a formula 2Ф(z)-1, in Excel =2*NORM.ST.DIST(A2;1)-1.

The diagram clearly shows the main basic properties of the normal distribution, including the three-sigma rule. Function NORM.ST.DIST. is an automatic table of normal distribution function values in Excel.
There may also be an inverse problem: according to the available probability P(Z
NORM.ST.REV function
NORM.ST.REV calculates the inverse of the standard normal distribution function. The syntax consists of one parameter:
=NORM.ST.REV(probability)
probability is a probability.
This formula is used as often as the previous one, because using the same tables you have to look not only for probabilities, but also for quantiles.

For example, when calculating confidence intervals, a confidence probability is specified, according to which it is necessary to calculate the value z.

Given that the confidence interval consists of an upper and lower limit and that the normal distribution is symmetrical around zero, it is enough to obtain the upper limit (positive deviation). The lower limit is taken with a negative sign. Let us denote the confidence probability as γ (gamma), then the upper limit of the confidence interval is calculated using the following formula.
![]()
Let's calculate the values in Excel z(which corresponds to the deviation from the average in sigma) for several probabilities, including those that any statistician knows by heart: 90%, 95% and 99%. In cell B2 we indicate the formula: =NORM.ST.REV((1+A2)/2). By changing the value of the variable (probability in cell A2), we obtain different boundaries of the intervals.

The 95% confidence interval is 1.96, that is, almost 2 standard deviations. From here it is easy, even mentally, to estimate the possible spread of a normal random variable. In general, the 90%, 95% and 99% confidence intervals correspond to confidence intervals of ±1.64, ±1.96 and ±2.58σ.
In general, the NORM.ST.DIST and NORM.ST.REV functions allow you to perform any calculation related to the normal distribution. But to make things easier and less complicated, Excel has several other features. For example, you can use CONFIDENCE NORM to calculate confidence intervals for the mean. To check the arithmetic mean there is the formula Z.TEST.
Let's look at a couple more useful formulas with examples.
NORMAL DIST function
Function NORMAL DIST. differs from NORM.ST.DIST. only because it is used to process data of any scale, and not just normalized ones. Normal distribution parameters are specified in the syntax.
=NORM.DIST(x,average,standard_deviation,integral)
average– mathematical expectation used as the first parameter of the normal distribution model
standard_off– standard deviation – the second parameter of the model
integral– if 0, then the density is calculated, if 1 – then the value of the function, i.e. P(X
For example, the density for the value 15, which was extracted from a normal sample with an expectation of 10, a standard deviation of 3, is calculated as follows:

If the last parameter is set to 1, then we get the probability that the normal random variable will be less than 15 for the given distribution parameters. Thus, probabilities can be calculated directly from the original data.
NORM.REV function
This is a quantile of the normal distribution, i.e. the value of the inverse function. The syntax is as follows.
=NORM.REV(probability,average,standard_deviation)
probability- probability
average– mathematical expectation
standard_off– standard deviation
The purpose is the same as NORM.ST.REV, only the function works with data of any scale.
An example is shown in the video at the end of the article.
Normal Distribution Modeling
Some problems require the generation of normal random numbers. There is no ready-made function for this. However, Excel has two functions that return random numbers: CASE BETWEEN And RAND. The first produces random, uniformly distributed integers within specified limits. The second function generates uniformly distributed random numbers between 0 and 1. To make an artificial sample with any given distribution, you need the function RAND.
Let's say that to conduct an experiment it is necessary to obtain a sample from a normally distributed population with an expectation of 10 and a standard deviation of 3. For one random value, we will write a formula in Excel.
NORM.INV(RAND();10;3)
Let's extend it to the required number of cells and the normal sample is ready.
To model standardized data, you should use NORM.ST.REV.
The process of converting uniform numbers to normal numbers can be shown in the following diagram. From the uniform probabilities that are generated by the RAND formula, horizontal lines are drawn to the graph of the normal distribution function. Then, from the points of intersection of the probabilities with the graph, projections are lowered onto the horizontal axis.
What else to read
THE LAST NOTES
- Andrey Shcheglov: Reformation in Sweden
- Vegan pumpkin stuffed with rice and baked whole in the oven
- Teleportation and time travel
- Notification of changes in the terms of the employment contract and transition to an effective contract Notification of the employee about the introduction of an effective contract
- Liquid buckwheat porridge - benefits in every spoon
