What are eigenvalues? Characteristic equation of a matrix. Linear operations on vectors

"The first part sets out the provisions that are minimally necessary for understanding chemometrics, and the second part contains the facts that you need to know for a deeper understanding of the methods of multivariate analysis. The presentation is illustrated with examples made in the Excel workbook Matrix.xls, which accompanies this document.

Links to examples are placed in the text as Excel objects. These examples are abstract in nature, they are in no way tied to tasks analytical chemistry. Real examples The uses of matrix algebra in chemometrics are discussed in other texts covering a variety of chemometric applications.

Most measurements made in analytical chemistry are not direct, but indirect. This means that in the experiment, instead of the value of the desired analyte C (concentration), another value is obtained x(signal), related but not equal to C, i.e. x(C) ≠ C. As a rule, the type of dependence x(C) is unknown, but fortunately in analytical chemistry most measurements are proportional. This means that with increasing concentration of C in a times, signal X will increase by the same amount, i.e. x(a C) = a x(C). In addition, the signals are also additive, so the signal from a sample in which two substances with concentrations C 1 and C 2 are present will be equal to the sum signals from each component, i.e. x(C 1 + C 2) = x(C 1)+ x(C 2). Proportionality and additivity together give linearity. Many examples can be given to illustrate the principle of linearity, but it is enough to mention the two most shining examples- chromatography and spectroscopy. The second feature inherent in an experiment in analytical chemistry is multichannel. Modern analytical equipment simultaneously measures signals for many channels. For example, the intensity of light transmission is measured for several wavelengths at once, i.e. range. Therefore, in the experiment we deal with many signals x 1 , x 2 ,...., x n, characterizing the set of concentrations C 1 , C 2 , ..., C m of substances present in the system under study.

Rice. 1 Spectra

So, an analytical experiment is characterized by linearity and multidimensionality. Therefore, it is convenient to consider experimental data as vectors and matrices and manipulate them using the apparatus of matrix algebra. The fruitfulness of this approach is illustrated by the example shown in, which presents three spectra taken at 200 wavelengths from 4000 to 4796 cm −1. The first (x 1) and second (x 2) spectra were obtained for standard samples in which the concentrations of two substances A and B are known: in the first sample [A] = 0.5, [B] = 0.1, and in the second sample [A] = 0.2, [B] = 0.6. What can be said about a new, unknown sample, the spectrum of which is designated x 3?

Let's consider three experimental spectra x 1, x 2 and x 3 as three vectors of dimension 200. Using linear algebra, we can easily show that x 3 = 0.1 x 1 +0.3 x 2, therefore, in the third sample, only substances A and B are obviously present in concentrations [A] = 0.5×0.1 + 0.2×0.3 = 0.11 and [B] = 0.1×0.1 + 0.6×0.3 = 0.19.

1. Basic information 1.1 Matrices

Matrix called a rectangular table of numbers, for example

Rice. 2 Matrix

Matrices are denoted by capital bold letters (A), and their elements by corresponding lowercase letters with indices, i.e. a ij. The first index numbers the rows, and the second - the columns. In chemometrics, it is customary to denote the maximum value of an index with the same letter as the index itself, but in capital letters. Therefore, matrix A can also be written as ( a ij , i = 1,..., I; j = 1,..., J). For the example matrix I = 4, J= 3 and a 23 = −7.5.

Pair of numbers I And J is called the dimension of the matrix and is denoted as I× J. An example of a matrix in chemometrics is a set of spectra obtained for I samples for J wavelengths.

1.2. The simplest operations with matrices

Matrices can be multiply by numbers. In this case, each element is multiplied by this number. For example -

Rice. 3 Multiplying a matrix by a number

Two matrices of the same dimension can be element by element fold And subtract. For example,

Rice. 4 Matrix addition

As a result of multiplication by a number and addition, a matrix of the same dimension is obtained.

A zero matrix is ​​a matrix consisting of zeros. It is denoted O. Obviously, A +O = A, A −A = O and 0A = O.

The matrix can be transpose. During this operation, the matrix is ​​flipped, i.e. rows and columns are swapped. Transposition is indicated by a prime, A" or subscript A t. Thus, if A = ( a ij , i = 1,..., I; j = 1,...,J), then A t = ( a ji , j = 1,...,J; i = 1,..., I). For example

Rice. 5 Matrix transposition

It is obvious that (A t) t = A, (A + B) t = A t + B t.

1.3. Matrix multiplication

Matrices can be multiply, but only if they have the appropriate dimensions. Why this is so will be clear from the definition. Product of matrix A, dimension I× K, and matrix B, dimension K× J, called matrix C, dimension I× J, whose elements are numbers

Thus, for the product AB it is necessary that the number of columns in the left matrix A be equal to the number of rows in the right matrix B. An example of a matrix product -

Fig.6 Product of matrices

The rule for matrix multiplication can be formulated as follows. In order to find an element of the matrix C at the intersection i-th line and j th column ( c ij) must be multiplied element by element i-th row of the first matrix A on j th column of the second matrix B and add all the results. So in the example shown, an element from the third row and second column is obtained as the sum of the element-wise products of the third row A and the second column B

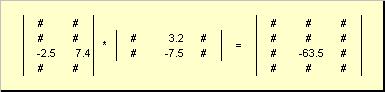
Fig.7 Element of the product of matrices

The product of matrices depends on the order, i.e. AB ≠ BA, at least for dimensional reasons. They say that it is non-commutative. However, the product of matrices is associative. This means that ABC = (AB)C = A(BC). In addition, it is also distributive, i.e. A (B +C) = AB +AC. Obviously AO = O.

1.4. Square matrices

If the number of matrix columns is equal to the number of its rows ( I = J=N), then such a matrix is ​​called square. In this section we will consider only such matrices. Among these matrices, matrices with special properties can be distinguished.

Single matrix (denoted I, and sometimes E) is a matrix in which all elements are equal to zero, with the exception of diagonal ones, which are equal to 1, i.e.

Obviously AI = IA = A.

The matrix is ​​called diagonal, if all its elements except diagonal ones ( a ii) are equal to zero. For example

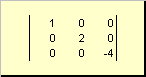
Rice. 8 Diagonal matrix

Matrix A is called upper triangular, if all its elements lying below the diagonal are equal to zero, i.e. a ij= 0, at i>j. For example

Rice. 9 Upper triangular matrix

The lower triangular matrix is ​​defined similarly.

Matrix A is called symmetrical, if A t = A . In other words a ij = a ji. For example

Rice. 10 Symmetric matrix

Matrix A is called orthogonal, If

A t A = AA t = I .

The matrix is ​​called normal If

1.5. Trace and determinant

Next square matrix A (denoted by Tr(A) or Sp(A)) is the sum of its diagonal elements,

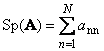
For example,

Rice. 11 Matrix trace

It's obvious that

Sp(α A ) = α Sp(A ) and

Sp(A +B) = Sp(A)+ Sp(B).

It can be shown that

Sp(A) = Sp(A t), Sp(I) = N,

and also that

Sp(AB) = Sp(BA).

Another important characteristic square matrix is ​​its determinant(denoted det(A )). Definition of determinant in general case quite complicated, so we will start with the simplest option - a matrix A of dimension (2x2). Then

For a (3×3) matrix the determinant will be equal to

In the case of the matrix ( N× N) the determinant is calculated as the sum 1·2·3· ... · N= N! terms, each of which is equal

Indexes k 1 , k 2 ,..., k N are defined as all possible ordered permutations r numbers in the set (1, 2, ..., N). Calculating the determinant of a matrix is ​​a complex procedure, which in practice is carried out using special programs. For example,

Rice. 12 Matrix determinant

Let us note only the obvious properties:

det(I ) = 1, det(A ) = det(A t),

det(AB) = det(A)det(B).

1.6. Vectors

If the matrix consists of only one column ( J= 1), then such an object is called vector. More precisely, a column vector. For example

One can also consider matrices consisting of one row, for example

This object is also a vector, but row vector. When analyzing data, it is important to understand which vectors we are dealing with - columns or rows. So the spectrum taken for one sample can be considered as a row vector. Then the set of spectral intensities at a certain wavelength for all samples should be treated as a column vector.

The dimension of a vector is the number of its elements.

It is clear that any column vector can be turned into a row vector by transposition, i.e.

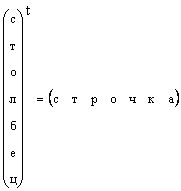
In cases where the shape of the vector is not specifically specified, but is simply said to be a vector, then they mean a column vector. We will also adhere to this rule. A vector is denoted by a lowercase, upright, bold letter. A zero vector is a vector all of whose elements are zero. It is designated 0.

1.7. The simplest operations with vectors

Vectors can be added and multiplied by numbers in the same way as matrices. For example,

Rice. 13 Operations with vectors

Two vectors x and y are called colinear, if there is a number α such that

1.8. Products of vectors

Two vectors of the same dimension N can be multiplied. Let there be two vectors x = ( x 1 , x 2 ,...,x N) t and y = ( y 1 , y 2 ,...,y N) t . Guided by the row-by-column multiplication rule, we can compose two products from them: x t y and xy t. First work

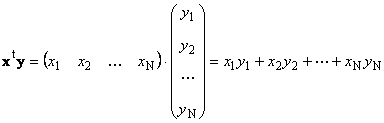
called scalar or internal. Its result is a number. The notation (x ,y )= x t y is also used for it. For example,

Rice. 14 Inner (scalar) product

Second piece

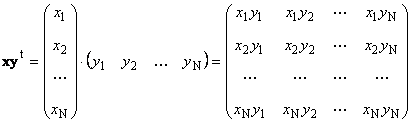
called external. Its result is a matrix of dimension ( N× N). For example,

Rice. 15 External work

Vectors whose scalar product is zero are called orthogonal.

1.9. Vector norm

The scalar product of a vector with itself is called a scalar square. This value

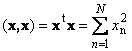
defines a square length vector x. To indicate length (also called the norm vector) the notation is used

For example,

Rice. 16 Vector norm

A vector of unit length (||x || = 1) is called normalized. A non-zero vector (x ≠ 0) can be normalized by dividing it by its length, i.e. x = ||x || (x/ ||x ||) = ||x || e. Here e = x/ ||x || - normalized vector.

Vectors are called orthonormal if they are all normalized and pairwise orthogonal.

1.10. Angle between vectors

The scalar product determines and cornerφ between two vectors x and y

If the vectors are orthogonal, then cosφ = 0 and φ = π/2, and if they are colinear, then cosφ = 1 and φ = 0.

1.11. Vector representation of a matrix

Each matrix A of size I× J can be represented as a set of vectors

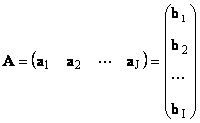
Here each vector a j is j th column, and the row vector b i is i th row of matrix A

1.12. Linearly dependent vectors

Vectors of the same dimension ( N) can be added and multiplied by a number, just like matrices. The result will be a vector of the same dimension. Let there be several vectors of the same dimension x 1, x 2,...,x K and the same number of numbers α α 1, α 2,...,α K. Vector

y = α 1 x 1 + α 2 x 2 +...+ α K x K

called linear combination vectors x k .

If there are such non-zero numbers α k ≠ 0, k = 1,..., K that y = 0, then such a set of vectors x k called linearly dependent. Otherwise, the vectors are said to be linearly independent. For example, vectors x 1 = (2, 2) t and x 2 = (−1, −1) t are linearly dependent, because x 1 +2x 2 = 0

1.13. Matrix rank

Consider a set of K vectors x 1 , x 2 ,...,x K dimensions N. The rank of this system of vectors is the maximum number of linearly independent vectors. For example in the set

there are only two linearly independent vectors, for example x 1 and x 2, so its rank is 2.

Obviously, if there are more vectors in a set than their dimension ( K>N), then they are necessarily linearly dependent.

Matrix rank(denoted by rank(A)) is the rank of the system of vectors of which it consists. Although any matrix can be represented in two ways (column or row vectors), this does not affect the rank value, because

1.14. inverse matrix

A square matrix A is called non-singular if it has a unique reverse matrix A -1 determined by the conditions

AA −1 = A −1 A = I .

The inverse matrix does not exist for all matrices. A necessary and sufficient condition for non-degeneracy is

det(A) ≠ 0 or rank(A) = N.

Matrix inversion is a complex procedure for which there are special programs. For example,

Rice. 17 Matrix inversion

Let us present the formulas for the simplest case - a 2×2 matrix

If matrices A and B are non-singular, then

(AB ) −1 = B −1 A −1 .

1.15. Pseudo inverse matrix

If the matrix A is singular and the inverse matrix does not exist, then in some cases you can use pseudoinverse matrix, which is defined as a matrix A+ such that

AA + A = A.

The pseudoinverse matrix is ​​not the only one and its form depends on the method of construction. For example, for a rectangular matrix you can use the Moore-Penrose method.

If the number of columns is less than the number of rows, then

A + =(A t A ) −1 A t

For example,

Rice. 17a Pseudo-inversion of a matrix

If the number of columns more number lines, then

A + =A t (AA t) −1

1.16. Multiplying a vector by a matrix

The vector x can be multiplied by a matrix A of suitable dimension. In this case, the column vector is multiplied on the right Ax, and the row vector is multiplied on the left x t A. If the vector dimension J, and the matrix dimension I× J then the result will be a vector of dimension I. For example,

Rice. 18 Multiplying a vector by a matrix

If the matrix A is square ( I× I), then the vector y = Ax has the same dimension as x. It's obvious that

A (α 1 x 1 + α 2 x 2) = α 1 Ax 1 + α 2 Ax 2 .

Therefore, matrices can be considered as linear transformations of vectors. In particular, Ix = x, Ox = 0.

2. Additional information 2.1. Systems of linear equations

Let A be a matrix of size I× J, and b is the dimension vector J. Consider the equation

Ax = b

relative to the vector x, dimension I. Essentially, it is a system of I linear equations with J unknown x 1 ,...,x J. A solution exists if and only if

rank(A) = rank(B) = R,

where B is the augmented dimension matrix I×( J+1), consisting of a matrix A complemented by a column b, B = (A b). Otherwise, the equations are inconsistent.

If R = I = J, then the solution is unique

x = A −1 b .

If R < I, then there are many different solutions that can be expressed through a linear combination J−R vectors. System homogeneous equations Ax = 0 with square matrix A ( N× N) has a nontrivial solution (x ≠ 0) if and only if det(A) = 0. If R= rank(A) 0.

Similarly defined negative(x t Ax< 0), non-negative(x t Ax ≥ 0) and negative(x t Ax ≤ 0) certain matrices.

2.4. Cholesky decomposition

If a symmetric matrix A is positive definite, then there is a unique triangular matrix U with positive elements for which

A = U t U .

For example,

Rice. 19 Cholesky decomposition

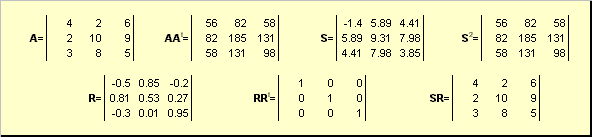
2.5. Polar decomposition

Let A be a non-singular square matrix of dimension N× N. Then there is a unique polar performance

A = SR,

where S is a non-negative symmetric matrix and R is an orthogonal matrix. Matrices S and R can be defined explicitly:

S 2 = AA t or S = (AA t) ½ and R = S −1 A = (AA t) −½ A .

For example,

Rice. 20 Polar decomposition

If the matrix A is singular, then the decomposition is not unique - namely: S is still one, but there can be many R. The polar decomposition represents the matrix A as a combination of compression/extension S and rotation R .

2.6. Eigenvectors and eigenvalues

Let A be a square matrix. The vector v is called eigenvector matrix A if

Av = λv,

where the number λ is called eigenvalue matrices A. Thus, the transformation that the matrix A performs on the vector v is reduced to a simple stretching or compression with a coefficient λ. The eigenvector is determined up to multiplication by a constant α ≠ 0, i.e. if v is an eigenvector, then αv is also an eigenvector.

2.7. Eigenvalues

The matrix A has dimension ( N× N) cannot be more than N eigenvalues. They satisfy characteristic equation

det(A − λI ) = 0,

which is an algebraic equation N-th order. In particular, for a 2×2 matrix the characteristic equation has the form

For example,

Rice. 21 Eigenvalues

Set of eigenvalues ​​λ 1 ,..., λ N matrix A is called spectrum A.

The spectrum has various properties. In particular

det(A ) = λ 1 ×...×λ N, Sp(A ) = λ 1 +...+λ N.

The eigenvalues ​​of an arbitrary matrix can be complex numbers, but if the matrix is ​​symmetric (A t = A), then its eigenvalues ​​are real.

2.8. Eigenvectors

The matrix A has dimension ( N× N) cannot be more than N eigenvectors, each of which corresponds to its own eigenvalue. To determine the eigenvector v n need to solve a system of homogeneous equations

(A − λ n I ) v n = 0 .

It has a nontrivial solution, since det(A − λ n I ) = 0.

For example,

Rice. 22 Eigenvectors

The eigenvectors of a symmetric matrix are orthogonal.

With matrix A, if there is a number l such that AX = lX.

In this case, the number l is called the eigenvalue of the operator (matrix A), corresponding to the vector X.

In other words, an eigenvector is a vector that, under the action of a linear operator, transforms into a collinear vector, i.e. just multiply by some number. Unlike him, no eigenvectors are more difficult to transform.

Let's write down the definition of an eigenvector in the form of a system of equations:

Let's move all the terms to the left side:

The latter system can be written as matrix form in the following way:

(A - lE)X = O

The resulting system always has a zero solution X = O. Such systems in which all free terms are equal to zero are called homogeneous. If the matrix of such a system is square and its determinant is not equal to zero, then using Cramer’s formulas we will always get a unique solution - zero. It can be proven that a system has non-zero solutions if and only if the determinant of this matrix is ​​equal to zero, i.e.

|A - lE| = = 0

This equation with unknown l is called the characteristic equation (characteristic polynomial) of the matrix A (linear operator).

It can be proven that the characteristic polynomial of a linear operator does not depend on the choice of basis.

For example, let's find the eigenvalues ​​and eigenvectors of the linear operator defined by the matrix A = .

To do this, let's create a characteristic equation |A - lE| = = (1 - l) 2 - 36 = 1 - 2l + l 2 - 36 = l 2 - 2l - 35 = 0; D = 4 + 140 = 144; eigenvalues ​​l 1 = (2 - 12)/2 = -5; l 2 = (2 + 12)/2 = 7.

To find eigenvectors, we solve two systems of equations

(A + 5E)X = O

(A - 7E)X = O

For the first of them, the expanded matrix takes the form

,

whence x 2 = c, x 1 + (2/3)c = 0; x 1 = -(2/3)s, i.e. X (1) = (-(2/3)s; s).

For the second of them, the expanded matrix takes the form

,

from where x 2 = c 1, x 1 - (2/3)c 1 = 0; x 1 = (2/3)s 1, i.e. X (2) = ((2/3)s 1; s 1).

Thus, the eigenvectors of this linear operator are all vectors of the form (-(2/3)с; с) with eigenvalue (-5) and all vectors of the form ((2/3)с 1 ; с 1) with eigenvalue 7 .

It can be proven that the matrix of the operator A in the basis consisting of its eigenvectors is diagonal and has the form:

,

where l i are the eigenvalues ​​of this matrix.

The converse is also true: if matrix A in some basis is diagonal, then all vectors of this basis will be eigenvectors of this matrix.

It can also be proven that if a linear operator has n pairwise distinct eigenvalues, then the corresponding eigenvectors are linearly independent, and the matrix of this operator in the corresponding basis has a diagonal form.

Let's illustrate this with the previous example. Let's take arbitrary non-zero values ​​c and c 1, but such that the vectors X (1) and X (2) are linearly independent, i.e. would form a basis. For example, let c = c 1 = 3, then X (1) = (-2; 3), X (2) = (2; 3).

Let's make sure linear independence these vectors:

12 ≠ 0. In this new basis, matrix A will take the form A * = .

To verify this, let's use the formula A * = C -1 AC. First, let's find C -1.

C -1 = ;

Quadratic shapes

The quadratic form f(x 1, x 2, x n) of n variables is a sum, each term of which is either the square of one of the variables, or the product of two different variables, taken with a certain coefficient: f(x 1, x 2, x n ) = (a ij = a ji).

The matrix A composed of these coefficients is called a matrix of quadratic form. This is always a symmetric matrix (i.e. a matrix symmetric about the main diagonal, a ij = a ji).

IN matrix notation the quadratic form is f(X) = X T AX, where

Indeed

For example, let's write the quadratic form in matrix form.

To do this, we find a matrix of quadratic form. Its diagonal elements are equal to the coefficients of the squared variables, and the remaining elements are equal to the halves of the corresponding coefficients of the quadratic form. That's why

Let the matrix-column of variables X be obtained by a non-degenerate linear transformation of the matrix-column Y, i.e. X = CY, where C is a non-singular matrix of nth order. Then the quadratic form f(X) = X T AX = (CY) T A(CY) = (Y T C T)A(CY) = Y T (C T AC)Y.

Thus, with a non-degenerate linear transformation C, the matrix of quadratic form takes the form: A * = C T AC.

For example, let's find the quadratic form f(y 1, y 2), obtained from the quadratic form f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 by linear transformation.

A quadratic form is called canonical (has a canonical form) if all its coefficients a ij = 0 for i ≠ j, i.e.
f(x 1, x 2, x n) = a 11 x 1 2 + a 22 x 2 2 + a nn x n 2 = .

Its matrix is ​​diagonal.

Theorem (proof not given here). Any quadratic form can be reduced to canonical form using a non-degenerate linear transformation.

For example, let us reduce the quadratic form to canonical form
f(x 1, x 2, x 3) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3.

To do this, first select a complete square with the variable x 1:

f(x 1, x 2, x 3) = 2(x 1 2 + 2x 1 x 2 + x 2 2) - 2x 2 2 - 3x 2 2 - x 2 x 3 = 2(x 1 + x 2) 2 - 5x 2 2 - x 2 x 3.

Now we select a complete square with the variable x 2:

f(x 1, x 2, x 3) = 2(x 1 + x 2) 2 - 5(x 2 2 + 2* x 2 *(1/10)x 3 + (1/100)x 3 2) + (5/100)x 3 2 =
= 2(x 1 + x 2) 2 - 5(x 2 - (1/10)x 3) 2 + (1/20)x 3 2.

Then the non-degenerate linear transformation y 1 = x 1 + x 2, y 2 = x 2 + (1/10)x 3 and y 3 = x 3 brings this quadratic form to the canonical form f(y 1, y 2, y 3) = 2y 1 2 - 5y 2 2 + (1/20)y 3 2 .

Note that the canonical form of a quadratic form is determined ambiguously (the same quadratic form can be reduced to the canonical form different ways). However, the received different ways canonical forms have a number of general properties. In particular, the number of terms with positive (negative) coefficients of a quadratic form does not depend on the method of reducing the form to this form (for example, in the example considered there will always be two negative and one positive coefficient). This property is called the law of inertia of quadratic forms.

Let us verify this by bringing the same quadratic form to canonical form in a different way. Let's start the transformation with the variable x 2:

f(x 1, x 2, x 3) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3 = -3x 2 2 - x 2 x 3 + 4x 1 x 2 + 2x 1 2 = - 3(x 2 2 +
+ 2* x 2 ((1/6) x 3 - (2/3)x 1) + ((1/6) x 3 - (2/3)x 1) 2) + 3((1/6) x 3 - (2/3)x 1) 2 + 2x 1 2 =
= -3(x 2 + (1/6) x 3 - (2/3)x 1) 2 + 3((1/6) x 3 + (2/3)x 1) 2 + 2x 1 2 = f (y 1 , y 2 , y 3) = -3y 1 2 -
+3y 2 2 + 2y 3 2, where y 1 = - (2/3)x 1 + x 2 + (1/6) x 3, y 2 = (2/3)x 1 + (1/6) x 3 and y 3 = x 1 . Here there is a negative coefficient -3 at y 1 and two positive coefficients 3 and 2 at y 2 and y 3 (and using another method we got a negative coefficient (-5) at y 2 and two positive ones: 2 at y 1 and 1/20 at y 3).

It should also be noted that the rank of a matrix of a quadratic form, called the rank of the quadratic form, equal to the number nonzero coefficients of the canonical form and does not change under linear transformations.

A quadratic form f(X) is called positive (negative) definite if for all values ​​of the variables that are not simultaneously equal to zero, it is positive, i.e. f(X) > 0 (negative, i.e.
f(X)< 0).

For example, the quadratic form f 1 (X) = x 1 2 + x 2 2 is positive definite, because is a sum of squares, and the quadratic form f 2 (X) = -x 1 2 + 2x 1 x 2 - x 2 2 is negative definite, because represents it can be represented as f 2 (X) = -(x 1 - x 2) 2.

In most practical situations, it is somewhat more difficult to establish the definite sign of a quadratic form, so for this we use one of the following theorems (we will formulate them without proof).

Theorem. A quadratic form is positive (negative) definite if and only if all eigenvalues ​​of its matrix are positive (negative).

Theorem (Sylvester criterion). A quadratic form is positive definite if and only if all the leading minors of the matrix of this form are positive.

The main (angular) minor of the kth order of the nth order matrix A is the determinant of the matrix, composed of the first k rows and columns of the matrix A ().

Note that for negative definite quadratic forms the signs of the principal minors alternate, and the first-order minor must be negative.

For example, let us examine the quadratic form f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 + 3x 2 2 for sign definiteness.

= (2 - l)*
*(3 - l) - 4 = (6 - 2l - 3l + l 2) - 4 = l 2 - 5l + 2 = 0; D = 25 - 8 = 17;
. Therefore, the quadratic form is positive definite.

Method 2. Principal minor of the first order of matrix A D 1 = a 11 = 2 > 0. Principal minor of the second order D 2 = = 6 - 4 = 2 > 0. Therefore, according to Sylvester’s criterion, the quadratic form is positive definite.

We examine another quadratic form for sign definiteness, f(x 1, x 2) = -2x 1 2 + 4x 1 x 2 - 3x 2 2.

Method 1. Let's construct a matrix of quadratic form A = . The characteristic equation will have the form = (-2 - l)*
*(-3 - l) - 4 = (6 + 2l + 3l + l 2) - 4 = l 2 + 5l + 2 = 0; D = 25 - 8 = 17;
. Therefore, the quadratic form is negative definite.

Method 2. Principal minor of the first order of matrix A D 1 = a 11 =
= -2 < 0. Главный минор второго порядка D 2 = = 6 - 4 = 2 >0. Consequently, according to Sylvester’s criterion, the quadratic form is negative definite (the signs of the main minors alternate, starting with the minus).

And as another example, we examine the sign-determined quadratic form f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2.

Method 1. Let's construct a matrix of quadratic form A = . The characteristic equation will have the form = (2 - l)*
*(-3 - l) - 4 = (-6 - 2l + 3l + l 2) - 4 = l 2 + l - 10 = 0; D = 1 + 40 = 41;
.

One of these numbers is negative and the other is positive. The signs of the eigenvalues ​​are different. Consequently, the quadratic form can be neither negatively nor positively definite, i.e. this quadratic form is not sign-definite (it can take values ​​of any sign).

Method 2. Principal minor of the first order of matrix A D 1 = a 11 = 2 > 0. Principal minor of the second order D 2 = = -6 - 4 = -10< 0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них - положителен).

How to insert mathematical formulas on a website?

If you ever need to add one or two mathematical formulas to a web page, then the easiest way to do this is as described in the article: mathematical formulas are easily inserted onto the site in the form of pictures that are automatically generated by Wolfram Alpha. In addition to simplicity, this universal method will help improve the visibility of the site in search engines. It has been working for a long time (and, I think, will work forever), but is already morally outdated.

If you regularly use mathematical formulas on your site, then I recommend you use MathJax - a special JavaScript library that displays mathematical notation in web browsers using MathML, LaTeX or ASCIIMathML markup.

There are two ways to start using MathJax: (1) using a simple code, you can quickly connect a MathJax script to your website, which will be automatically loaded from a remote server at the right time (list of servers); (2) download the MathJax script from a remote server to your server and connect it to all pages of your site. The second method - more complex and time-consuming - will speed up the loading of your site's pages, and if the parent MathJax server becomes temporarily unavailable for some reason, this will not affect your own site in any way. Despite these advantages, I chose the first method as it is simpler, faster and does not require technical skills. Follow my example, and in just 5 minutes you will be able to use all the features of MathJax on your site.

You can connect the MathJax library script from a remote server using two code options taken from the main MathJax website or on the documentation page:

One of these code options needs to be copied and pasted into the code of your web page, preferably between tags and or immediately after the tag. According to the first option, MathJax loads faster and slows down the page less. But the second option automatically monitors and loads the latest versions of MathJax. If you insert the first code, it will need to be updated periodically. If you insert the second code, the pages will load more slowly, but you will not need to constantly monitor MathJax updates.

The easiest way to connect MathJax is in Blogger or WordPress: in the site control panel, add a widget designed to insert third-party JavaScript code, copy the first or second version of the download code presented above into it, and place the widget closer to the beginning of the template (by the way, this is not at all necessary , since the MathJax script is loaded asynchronously). That's all. Now learn the markup syntax of MathML, LaTeX, and ASCIIMathML, and you are ready to insert mathematical formulas into your site's web pages.

Any fractal is constructed according to a certain rule, which is consistently applied an unlimited number of times. Each such time is called an iteration.

The iterative algorithm for constructing a Menger sponge is quite simple: the original cube with side 1 is divided by planes parallel to its faces into 27 equal cubes. One central cube and 6 cubes adjacent to it along the faces are removed from it. The result is a set consisting of the remaining 20 smaller cubes. Doing the same with each of these cubes, we get a set consisting of 400 smaller cubes. Continuing this process endlessly, we get a Menger sponge.

SYSTEM OF HOMOGENEOUS LINEAR EQUATIONS

A system of homogeneous linear equations is a system of the form

It is clear that in this case , because all elements of one of the columns in these determinants are equal to zero.

Since the unknowns are found according to the formulas , then in the case when Δ ≠ 0, the system has a unique zero solution x = y = z= 0. However, in many problems the interesting question is whether a homogeneous system has solutions other than zero.

Theorem. In order for a system of linear homogeneous equations to have a non-zero solution, it is necessary and sufficient that Δ ≠ 0.

So, if the determinant Δ ≠ 0, then the system has a unique solution. If Δ ≠ 0, then the system of linear homogeneous equations has an infinite number of solutions.

Examples.

Eigenvectors and eigenvalues ​​of a matrix

Let a square matrix be given , X– some matrix-column, the height of which coincides with the order of the matrix A. .

In many problems we have to consider the equation for X

where λ is a certain number. It is clear that for any λ this equation has a zero solution.

The number λ for which this equation has non-zero solutions is called eigenvalue matrices A, A X for such λ is called eigenvector matrices A.

Let's find the eigenvector of the matrix A. Because the E∙X = X, then the matrix equation can be rewritten as or . In expanded form, this equation can be rewritten as a system of linear equations. Really .

And therefore

So, we have obtained a system of homogeneous linear equations for determining the coordinates x 1, x 2, x 3 vector X. For a system to have non-zero solutions it is necessary and sufficient that the determinant of the system be equal to zero, i.e.

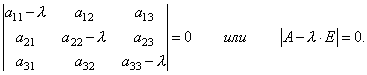
This is a 3rd degree equation for λ. It's called characteristic equation matrices A and serves to determine the eigenvalues ​​of λ.

Each eigenvalue λ corresponds to an eigenvector X, whose coordinates are determined from the system at the corresponding value of λ.

Examples.

VECTOR ALGEBRA. THE CONCEPT OF VECTOR

When studying various branches of physics, there are quantities that are completely determined by specifying their numerical values, for example, length, area, mass, temperature, etc. Such quantities are called scalar. However, in addition to them, there are also quantities, to determine which, in addition to the numerical value, it is also necessary to know their direction in space, for example, the force acting on the body, the speed and acceleration of the body when it moves in space, tension magnetic field at a given point in space, etc. Such quantities are called vector quantities.

Let us introduce a strict definition.

Directed segment Let's call a segment, relative to the ends of which it is known which of them is the first and which is the second.

Vector called a directed segment having a certain length, i.e. This is a segment of a certain length, in which one of the points limiting it is taken as the beginning, and the second as the end. If A– the beginning of the vector, B is its end, then the vector is denoted by the symbol; in addition, the vector is often denoted by a single letter. In the figure, the vector is indicated by a segment, and its direction by an arrow.

Module or length A vector is called the length of the directed segment that defines it. Denoted by || or ||.

We will also include the so-called zero vector, whose beginning and end coincide, as vectors. It is designated. The zero vector does not have a specific direction and its modulus is zero ||=0.

Vectors are called collinear, if they are located on the same line or on parallel lines. Moreover, if the vectors and are in the same direction, we will write , opposite.

Vectors located on straight lines parallel to the same plane are called coplanar.

The two vectors are called equal, if they are collinear, have the same direction and are equal in length. In this case they write .

From the definition of equality of vectors it follows that a vector can be transported parallel to itself, placing its origin at any point in space.

For example .

LINEAR OPERATIONS ON VECTORS

Multiplying a vector by a number.

The product of a vector and the number λ is a new vector such that:

The product of a vector and a number λ is denoted by .

For example, there is a vector directed in the same direction as the vector and having a length half as large as the vector.

The introduced operation has the following properties:

Vector addition.

Let and be two arbitrary vectors. Let's take an arbitrary point O and construct a vector. After that from the point A let's put aside the vector. The vector connecting the beginning of the first vector with the end of the second is called amount of these vectors and is denoted .

The formulated definition of vector addition is called parallelogram rule, since the same sum of vectors can be obtained as follows. Let's postpone from the point O vectors and . Let's construct a parallelogram on these vectors OABC. Since vectors, then vector, which is a diagonal of a parallelogram drawn from the vertex O, will obviously be a sum of vectors.

It is easy to check the following properties of vector addition.

Vector difference.

A vector collinear to a given vector, equal in length and oppositely directed, is called opposite vector for a vector and is denoted by . The opposite vector can be considered as the result of multiplying the vector by the number λ = –1: .

Diagonal matrices have the simplest structure. The question arises whether it is possible to find a basis in which the matrix of the linear operator would have a diagonal form. Such a basis exists.
Let us be given a linear space R n and a linear operator A acting in it; in this case, operator A takes R n into itself, that is, A:R n → R n .

Definition. A non-zero vector x is called an eigenvector of the operator A if the operator A transforms x into a collinear vector, that is. The number λ is called the eigenvalue or eigenvalue of the operator A, corresponding to the eigenvector x.
Let us note some properties of eigenvalues ​​and eigenvectors.
1. Any linear combination of eigenvectors operator A corresponding to the same eigenvalue λ is an eigenvector with the same eigenvalue.
2. Eigenvectors operator A with pairwise different eigenvalues ​​λ 1 , λ 2 , …, λ m are linearly independent.
3. If the eigenvalues ​​λ 1 =λ 2 = λ m = λ, then the eigenvalue λ corresponds to no more than m linearly independent eigenvectors.

So, if there are n linearly independent eigenvectors , corresponding to different eigenvalues ​​λ 1, λ 2, ..., λ n, then they are linearly independent, therefore, they can be taken as the basis of the space R n. Let us find the form of the matrix of the linear operator A in the basis of its eigenvectors, for which we will act with the operator A on the basis vectors: Then .
Thus, the matrix of the linear operator A in the basis of its eigenvectors has a diagonal form, and the eigenvalues ​​of the operator A are along the diagonal.
Is there another basis in which the matrix has a diagonal form? The answer to this question is given by the following theorem.

Theorem. The matrix of a linear operator A in the basis (i = 1..n) has a diagonal form if and only if all the vectors of the basis are eigenvectors of the operator A.

Rule for finding eigenvalues ​​and eigenvectors Let a vector be given , where x 1 , x 2 , …, x n are the coordinates of the vector x relative to the basis and x is the eigenvector of the linear operator A corresponding to the eigenvalue λ, that is. This relationship can be written in matrix form

. (*)

Equation (*) can be considered as an equation for finding x, and , that is, we are interested in non-trivial solutions, since the eigenvector cannot be zero. It is known that nontrivial solutions of a homogeneous system of linear equations exist if and only if det(A - λE) = 0. Thus, for λ to be an eigenvalue of the operator A it is necessary and sufficient that det(A - λE) = 0.
If equation (*) is written in detail in coordinate form, we obtain a system of linear homogeneous equations:

(1)
Where - linear operator matrix.

System (1) has a non-zero solution if its determinant D is equal to zero

We received an equation for finding eigenvalues.
This equation is called the characteristic equation, and its left side is called the characteristic polynomial of the matrix (operator) A. If the characteristic polynomial has no real roots, then the matrix A has no eigenvectors and cannot be reduced to diagonal form.
Let λ 1, λ 2, …, λ n be the real roots of the characteristic equation, and among them there may be multiples. Substituting these values ​​in turn into system (1), we find the eigenvectors.

Example 12. The linear operator A acts in R 3 according to the law, where x 1, x 2, .., x n are the coordinates of the vector in the basis , , . Find the eigenvalues ​​and eigenvectors of this operator.
Solution. We build the matrix of this operator:
.
We create a system for determining the coordinates of eigenvectors:

We compose a characteristic equation and solve it:

.
λ 1,2 = -1, λ 3 = 3.
Substituting λ = -1 into the system, we have:
or
Because , then there are two dependent variables and one free variable.
Let x 1 be a free unknown, then We solve this system in any way and find the general solution of this system: The fundamental system of solutions consists of one solution, since n - r = 3 - 2 = 1.
The set of eigenvectors corresponding to the eigenvalue λ = -1 has the form: , where x 1 is any number other than zero. Let's choose one vector from this set, for example, putting x 1 = 1: .
Reasoning similarly, we find the eigenvector corresponding to the eigenvalue λ = 3: .
In the space R 3, the basis consists of three linearly independent vectors, but we received only two linearly independent eigenvectors, from which the basis in R 3 cannot be composed. Consequently, we cannot reduce the matrix A of a linear operator to diagonal form.

Example 13. Given a matrix .
1. Prove that the vector is an eigenvector of matrix A. Find the eigenvalue corresponding to this eigenvector.
2. Find a basis in which matrix A has a diagonal form.
Solution.
1. If , then x is an eigenvector

.
Vector (1, 8, -1) is an eigenvector. Eigenvalue λ = -1.
The matrix has a diagonal form in a basis consisting of eigenvectors. One of them is famous. Let's find the rest.
We look for eigenvectors from the system:

Characteristic equation: ;
(3 + λ)[-2(2-λ)(2+λ)+3] = 0; (3+λ)(λ 2 - 1) = 0
λ 1 = -3, λ 2 = 1, λ 3 = -1.
Let's find the eigenvector corresponding to the eigenvalue λ = -3:

The rank of the matrix of this system is two and equal to the number of unknowns, so this system has only a zero solution x 1 = x 3 = 0. x 2 here can be anything other than zero, for example, x 2 = 1. Thus, the vector (0 ,1,0) is an eigenvector corresponding to λ = -3. Let's check:
.
If λ = 1, then we obtain the system
The rank of the matrix is ​​two. We cross out the last equation.
Let x 3 be a free unknown. Then x 1 = -3x 3, 4x 2 = 10x 1 - 6x 3 = -30x 3 - 6x 3, x 2 = -9x 3.
Assuming x 3 = 1, we have (-3,-9,1) - an eigenvector corresponding to the eigenvalue λ = 1. Check:

.
Since the eigenvalues ​​are real and distinct, the vectors corresponding to them are linearly independent, so they can be taken as a basis in R 3 . Thus, in the basis , , matrix A has the form:
.
Not every matrix of a linear operator A:R n → R n can be reduced to diagonal form, since for some linear operators there may be less than n linear independent eigenvectors. However, if the matrix is ​​symmetric, then the root of the characteristic equation of multiplicity m corresponds to exactly m linearly independent vectors.

Definition. A symmetric matrix is ​​a square matrix in which the elements symmetric about the main diagonal are equal, that is, in which .
Notes. 1. All eigenvalues ​​of a symmetric matrix are real.
2. The eigenvectors of a symmetric matrix corresponding to pairwise different eigenvalues ​​are orthogonal.
As one of the many applications of the studied apparatus, we consider the problem of determining the type of a second-order curve.