Odredite masu hemisfere s površinskom gustoćom. Raspored granica integracije pri prijelazu na niz od tri integrala. Fizičke primjene površinskih integrala

Rad na terenu

Rad pri gibanju tijela u polju sila po krivulji C izražava se krivolinijskim integralom druge vrste

gdje je sila koja djeluje na tijelo, jedinični tangentni vektor (slika 1). Oznaka znači skalarni produkt vektora i .

Imajte na umu da polje sile nije nužno uzrok gibanja tijela. Tijelo se može kretati pod utjecajem druge sile. U tom slučaju rad sile ponekad može biti negativan.

Ako je vektorsko polje navedeno u koordinatnom obliku u obrascu

tada se terenski rad računa po formuli

U posebnom slučaju kada se tijelo giba po ravninskoj krivulji C u O ravnini xy, formula je važeća

Gdje

Ako je putanja C definiran preko parametra t (tčesto znači vrijeme), tada formula za izračun rada poprima oblik

Gdje t varira u rasponu od α prije β . Ako vektorsko polje potencijalno, zatim rad učinjen za pomicanje tijela iz točke A točno B izražen formulom

Gdje je potencijal polja.

Sl. 1		sl.2

Amperov zakon

Krivuljasti integral magnetskog polja s indukcijom duž zatvorene petlje C proporcionalna ukupnoj struji koja teče kroz područje ograničeno krugom C(Slika 2). To se izražava formulom

Gdje - magnetska permeabilnost vakuuma, jednako N/m.

Faradayev zakon

Elektromotorna sila ε induciran u zatvorenoj petlji C, jednaka brzini promjene magnetskog toka ψ , prolazeći kroz ovu konturu (slika 3).

sl.3

Primjer

Odredite masu žice u obliku odsječka iz točke A(1,1) do B(2.4). Masa je raspoređena duž segmenta s gustoćom.

Riješenje. Sastavimo najprije parametarsku jednadžbu pravca AB.

gdje je parametar t varira u intervalu. Tada je masa žice

2.4 Fizičke primjene površinskih integrala

Površinski integrali koriste se u mnogim primijenjenim proračunima. Konkretno, koriste se za izračunavanje

Masa školjke;

Središte mase i momenti tromosti ljuske;

Sila privlačenja i sila pritiska;

Strujanje tekućine i tvari kroz površinu;

Električni naboj raspoređen po površini;

Električna polja (Gaussov teorem u elektrostatici).

Masa školjke

Neka S To je tanka, glatka ljuska. Raspodjela mase ljuske opisuje se funkcijom gustoće. Zatim dovršite masa ljuske izražava se preko površinskog integrala prve vrste prema formuli

Središte mase i momenti tromosti ljuske

Neka raspodjela mase m u tankoj ljusci opisuje se kontinuiranom funkcijom gustoće. Koordinate središte mase ljuske određuju se formulama

− tzv momenti prvog reda oko koordinatnih ravnina x = 0, y = 0 i z = 0, odnosno.

Momenti tromosti ljuske u odnosu na osi Ox, Oy, Oz izražavaju se, redom, formulama

Momenti tromosti ljuske u odnosu na ravnine xy, yz, xz određuju se formulama

Površinska gravitacija

Neka površina bude dana S, au točki ( x 0 , g 0 , z 0), koji ne pripada površini, postoji tijelo mase m(slika 1).

Sl. 1		sl.2

Sila gravitacije između površine S i točkasto tijelo m određuje se izrazom

Gdje , G- gravitacijska konstanta, - funkcija gustoće.

Sila pritiska

Pretpostavimo da površina S zadan je vektorom i pod utjecajem je neke sile pritiska (to može biti brana, krilo aviona, stijenka cilindra sa stlačenim plinom itd.). Ukupna sila koju stvara pritisak nalazi se korištenjem površinskog integrala prema formuli

Tlak, po definiciji, djeluje u smjeru vektora normale na površinu S u svakoj točki. Stoga možemo pisati

gdje je jedinični vektor normale na površinu S.

Strujanje fluida i strujanje tvari

Ako se brzina tekućine promatra kao vektorsko polje, tada je protok kroz površinu S nazvao protok tekućine. Jednaka je volumenu tekućine koja prolazi kroz površinu S po jedinici vremena i izražava se formulom

Slično se naziva tok vektorskog polja, gdje je ρ gustoća protok materije a određena je izrazom

On je brojčano jednaka masi tvari koja prolazi kroz površinu S po jedinici vremena.

Površinski naboj

Neka je količina gustoća raspodjele naboja po površini. Zatim puna naplatiti, raspoređen po vodljivoj površini S izražen formulom

Gaussov teorem

Tok električnog pomaka kroz zatvorenu površinu S jednak algebarskom zbroju svih naboja unutar površine:

gdje je jakost električnog polja, ε − relativna dielektrična konstanta medija, − dielektrična konstanta vakuuma.
Gaussov teorem vrijedi za sve zatvorene površine. U slučaju površine s dovoljnom simetrijom, ovaj teorem pojednostavljuje izračun električnog polja. Gaussov teorem smatra se jednim od glavnih postulata teorije elektriciteta. Uvršten je u sustav Maxwellovih osnovnih jednadžbi.

Primjer

Nađite masu parabolične ljuske dane jednadžbom koja ima gustoću.

Riješenje.

Upotrijebimo formulu

Projekcija D(x,y) parabolična površina S do aviona xy je kružnica polumjera 1 sa središtem u ishodištu. Stoga možemo pisati

Prelaskom na polarne koordinate u integrandu dobivamo

Napravimo zamjenu. Zatim . Ovdje u = 1 at r = 0, i na r = 1. Dakle, integral je jednak

Knjiga >> Građevinarstvo

Legure su dvostruko, trostruke i više složeni sustavi... volumetrijska težina. Tjelesno, ovaj stav pokazuje... ponekad podvrgnut površan strojna obrada: ... u prilogu u podupiračima. Tako, potrebne uvjete geometrijski ...

Psihološki rječnik

Knjiga >> Psihologija

Iritacije u geometrijski progresija odgovara... vrsti sastavni: 1) ... simetrija; 4) krivocrtnost(u M. str. ... na globalnoj razini. U primjena osobi P. p. ... fizički senzacije. Brzo površan...znanost sa dvostruko ili utrostručiti"državljanstvo", ...

Trostruki integral se piše na sljedeći način:

Izračunajte trostruki integral - znači pronaći broj jednak volumenu tijela V ili, što je isto - područja V .

Gotovo svatko može razumjeti značenje izračuna trostrukog integrala "na teži način". Točnije - "ispod kože", a još preciznije - u njegovim dišnim organima - plućima. Bez obzira znate li to ili ne, u ljudskim plućima postoji više od 700 milijuna alveola - vezikularnih tvorevina isprepletenih mrežom kapilara. Razmjena plinova odvija se kroz stijenke alveola. Stoga možemo razmišljati ovako: volumen plina u plućima može se prikazati kao neka kompaktna površina. A ovaj se volumen sastoji od malih volumena koncentriranih u alveolama. Glavna uloga u ovoj usporedbi veliku ulogu igra golemi broj alveola u plućima: kao što ćemo vidjeti u sljedećem odlomku, kroz takav “veliki broj malih stvari” matematički je formuliran koncept trostrukog integrala.

Zašto se za određivanje volumena tijela koristi trostruki integral? V? Neka područje V podijeljen u n proizvoljna područja Δ vja, a ova oznaka ne označava samo svako malo područje, već i njegov volumen. U svakom tako malom području odabire se proizvoljna točka Mja, A f(Mi)- vrijednost funkcije f(M) u ovom trenutku. Sada ćemo maksimalno povećati broj takvih malih područja, i najveći promjer Δ vja- naprotiv, smanjiti. Možemo sastaviti integralni zbroj oblika

Ako funkcija f(M) = f(x, g, z) je kontinuirano, postojat će granica integralnog zbroja tip koji je gore naveden. Ova granica se zove trostruki integral .

U ovom slučaju funkcija f(M) = f(x, g, z) nazvan domenski integrabilan V ; V- područje integracije; x, g, z- integracijske varijable, dv(ili dx dy dz ) - element volumena.

Izračunavanje trostrukog integrala redukcijom višestrukosti

Kao i kod dvostrukih integrala, izračun trostrukih integrala svodi se na izračun integrala nižeg višestrukosti.

Razmotrimo trodimenzionalnu regiju V. Odozgo i odozgo (odnosno po visini) ovo je područje ograničeno plohama z = z1 (x, g) I z = z2 (x, g) . Na stranama (to jest, u širini), područje je ograničeno površinama g = g1 (x) I g = g2 (x) . I na kraju, u dubinu (ako područje gledate u smjeru osi Vol) - površine x = a I x = b

Za primjenu prijelaza na integrale nižeg višestrukosti potrebno je da trodimenzionalna domena V bio točan. Točno je kada je pravac paralelan s osi Oz, prelazi granicu regije V na ne više od dvije točke. Ispravna trodimenzionalna područja su, na primjer, kuboidan, elipsoid, tetraedar. Na donjoj slici prikazan je pravokutni paralelopiped s kojim ćemo se susresti u prvom primjeru rješavanja problema.

Da bismo vizualizirali razliku između ispravnosti i neispravnosti, dodajemo da plohe regije duž visine ispravne regije ne smiju biti konkavne prema unutra. Donja slika je primjer netočnog područja V- jednolistni hiperboloid, čija je površina ravna, paralelna s osi Oz(crveno), siječe se u više od dvije točke.

Razmotrit ćemo samo ispravna područja.

Dakle područje V- točno. Zatim za bilo koju funkciju f(x, g, z) , kontinuirano u regiji V, formula je važeća

Ova vam formula omogućuje smanjenje izračuna trostrukog integrala na sekvencijalni izračun unutarnjeg određenog integrala nad varijablom z(konstantno x I g) i vanjski dvostruki integral nad dvodimenzionalnom domenom D .

Prelazeći s dvostrukog integrala na ponovljeni, dobivamo sljedeću formulu za izračunavanje trostrukog integrala:

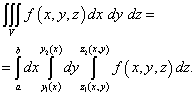
Dakle, da biste izračunali trostruki integral, trebate uzastopno izračunati tri određena integrala.

Ovi integrali se izračunavaju od najunutarnjih (preko varijable z) do najudaljenijeg (po varijabli x). Kako bi slijed izračuna bio lakši za razumijevanje, tri "ugniježđena" integrala mogu se napisati na sljedeći način:

.

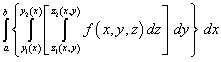Iz ovog unosa je već jasno da:

• prvo morate integrirati funkciju f(x, g, z) po varijabli z, i uzmite jednadžbe kao granice integracije z = z1 (x, g) I z = z2 (x, g) površine koje ograničavaju područje V ispod i iznad;
• g g = g1 (x) I g = g2 (x) površine koje ograničavaju područje V sa strana;
• integrirati rezultat dobiven u prethodnom koraku preko varijable x, i uzmite jednadžbe kao granice integracije x = a I x = b površine koje ograničavaju područje V u dubinu.

Primjer 1. Prijeđimo s trostrukog integrala na iterirani integral

-

niz od tri određeni integrali. Procijenite ovaj iterirani integral.

Riješenje. Izračun iteriranog integrala uvijek počinje od posljednjeg integrala:

.

Izračunajmo drugi integral – nad varijablom g:

.

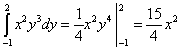x:

.

Odgovor: Ovaj ponovljeni integral i njemu odgovarajući trostruki integral jednaki su 10.

Primjer 2. Izračunajte trostruki integral

,

Gdje V- paralelopiped omeđen ravninama x = − 1 , x = + 1 , g = 0 , g = 1 , z = 0 , z = 2 .

Riješenje. Granice integracije za sva tri određena integrala jedinstveno su određene jednadžbama ploha koje omeđuju paralelepiped. Stoga ovaj trostruki integral odmah reduciramo na niz od tri određena integrala:

.

z

.

Integral izračunavamo “u sredini” - preko varijable g. Dobivamo;

.

Sada izračunavamo vanjski integral - preko varijable x:

Odgovor: Ovaj trostruki integral je -2.

Primjer 3. Izračunajte trostruki integral

,

Gdje Vx + g + z = 1 i koordinatne ravnine x = 0 , g = 0 , z= 0 . Regija V projiciran na ravninu xOy u trokut D, kao što je prikazano na donjoj slici.

Riješenje. Prvo postavimo granice integracije. Za integral po varijabli z donja granica integracije je jedinstveno određena: z= 0 . Da bismo dobili gornju granicu, izražavamo z iz x + g + z = 1 . Dobivamo 1 − x − g. Za integral po varijabli g donja granica integracije je jedinstveno određena: g= 0 . Da bismo dobili gornju granicu, izražavamo g iz x + g + z = 1 , s obzirom na to z= 0 (jer se pravac nalazi u ravnini xOy). Dobivamo: 1 − x .

Ovaj trostruki integral reduciramo na niz od tri određena integrala:

.

Izračunavamo najunutarnji integral - nad varijablom z, uzimajući u obzir x i y konstante. Dobivamo:

.

g. Dobivamo:

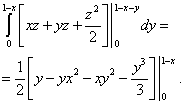
x:

Odgovor: Ovaj trostruki integral jednak je 1/8.

Izračunajte sami trostruki integral pa pogledajte rješenje

Primjer 4. Izračunajte trostruki integral

,

Gdje V- piramida omeđena ravninom x + g + z = 1 i koordinatne ravnine x = 0 , g = 0 , z = 0 .

Raspored granica integracije pri prijelazu na niz od tri integrala

Dešava se da se učenici koji nemaju posebnih poteškoća s izravnim računanjem integrala ne mogu naviknuti na postavljanje granica integracije pri prijelazu s trostrukog integrala na niz od tri određena integrala. Ova stvar zahtijeva određenu obuku. U prvom primjeru domena integracije V bio paralelepiped, s kojim je sve jasno: sa svih je strana omeđen ravninama, što znači da su granice integracije jednoznačno definirane jednadžbama ravnina. U drugom primjeru - piramida: ovdje je već trebalo malo više razmisliti i izraziti jednu od granica iz jednadžbe. A ako područje V jesu li ograničeni neravnim površinama? Naravno, potrebno je na određeni način pregledati područje V .

Počnimo s "strašnijim" primjerom kako bismo osjetili "situaciju blizu borbe".

Primjer 5. Rasporedite granice integracije pri prelasku iz trostrukog integrala, u kojem je regija V- elipsoid

.

Riješenje. Neka središte elipsoida bude ishodište, kao što je prikazano na gornjoj slici. Pogledajmo elipsoid odozdo. Odozdo je ograničen plohom koja je onaj dio plohe elipsoida koji se nalazi ispod ravnine xOy z a dobiveni izraz s predznakom minus bit će donja granica integracije nad varijablom z:

.

Sada pogledajmo elipsoid odozgo. Ovdje je ograničena plohom, a to je onaj dio elipsoidne plohe koji se nalazi iznad osi xOy. Stoga moramo izraziti iz jednadžbe elipsoida z a dobiveni izraz bit će gornja granica integracije nad varijablom z:

.

Projekcija elipsoida na ravninu xOy je elipsoid. Njegova jednadžba:

Da bi se dobila donja granica integracije nad varijablom g, treba izraziti g iz jednadžbe elipsoida i uzeti dobiveni izraz s predznakom minus:

.

Za gornju granicu integracije po varijabli g isti izraz sa znakom plus:

Što se tiče integracije preko varijable x, zatim područje V ograničeno po dubini ravninama. Prema tome, granice integracije nad varijablom x mogu se prikazati kao koordinate stražnje i prednje granice područja. U slučaju elipsoida, oni će se uzeti s negativnim i pozitivni znakovi duljine osovina a: x1 = − a I x2 = a .

Dakle, niz integrala za izračunavanje volumena elipsoida je sljedeći:

,

gdje su "yrek prvi", "yrek drugi", "zet prvi" i "zet drugi" gore dobiveni izrazi. Ako imate želju i hrabrost izračunati ovaj integral, a time i volumen elipsoida, onda je odgovor: 4 πabc/3 .

Sljedeći primjeri nisu tako strašni kao ovaj o kojem smo upravo govorili. Štoviše, oni uključuju ne samo postavljanje granica integracije, već i izračun samog trostrukog integrala. Provjerite što ste naučili slijedeći rješenje zastrašujućeg primjera. Još uvijek morate razmišljati kada postavljate granice.

Primjer 6. Izračunajte trostruki integral

ako je domena integracije ograničena ravninama x + g = 1 , x + 2g = 4 , g = 0 , g = 1 , z = 1 , z = 5 .

Riješenje. Primjer "odmarališta" uspoređuje se s primjerom 5, budući da su granice integracije preko "Y" i "Z" jedinstveno definirane. Ali morat ćemo se pozabaviti granicama integracije preko "X". Projekcija domene integracije na ravninu xOy je trapez ABCD.

U ovom primjeru, bolje je projicirati trapez na os Joj, inače, da biste izračunali trostruki integral, morat ćete podijeliti lik na tri dijela. U primjeru 4 počeli smo ispitivati ​​integracijsku regiju odozdo, a to je uobičajeni postupak. Ali u ovom primjeru počinjemo pregled sa strane ili, ako je lakše, stavljamo figuru na stranu i smatramo da je gledamo odozdo. Možemo pronaći granice integracije preko "X" čisto algebarski. Da bismo to učinili, izražavamo "x" iz prve i druge jednadžbe dane u primjeru uvjeta. Iz prve jednadžbe dobivamo donju granicu 1 − g, od drugog - gornji 4 − 2 g. Svedimo ovaj trostruki integral na niz od tri određena integrala:

.

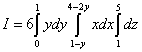Pažnja! U ovom primjeru, najudaljeniji integral nije nad varijablom "x", već nad varijablom "y", a integral "prosjeka" je nad varijablom "x"! Ovdje smo primijenili promjenu redoslijeda integracije s kojom smo se upoznali proučavajući dvostruki integral. To je zbog činjenice da smo, kao što je već spomenuto, počeli ispitivati ​​integracijsku regiju ne odozdo, već sa strane, to jest, nismo je projicirali na os Vol, po osi Joj.

Izračunavamo najunutarnji integral - nad varijablom z, uzimajući u obzir x i y konstante. Dobivamo:

Računamo prosječni integral – preko varijable x. Dobivamo:

.

Na kraju izračunavamo vanjski integral - preko varijable g:

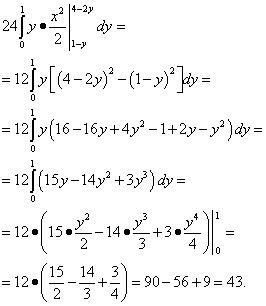
Odgovor: Ovaj trostruki integral jednak je 43.

Primjer 7. Izračunajte trostruki integral

,

ako je područje integracije ograničeno na površine x = 0 , g = 0 , z = 2 , x + g + z = 4 .

Riješenje. Regija V(piramida MNRP) je točno. Područje projekcije V do aviona xOy je trokut AOB.

Donje granice integracije za sve varijable navedene su u primjeru uvjeta. Nađimo gornju granicu integracije preko "X". Da bismo to učinili, izražavamo "x" iz četvrte jednadžbe, smatrajući "y" jednakim nuli i "ze" jednakim dva. Dobivamo x= 2. Pronađimo gornju granicu integracije preko "igre". Da bismo to učinili, izrazimo "Y" iz iste četvrte jednadžbe, smatrajući da je "Z" jednako dva, a "X" promjenjiva vrijednost. Dobivamo g = 2 − x. I konačno, nalazimo gornju granicu integracije preko varijable “z”. Da bismo to učinili, izrazimo "zet" iz iste četvrte jednadžbe, smatrajući "y" i "zet" promjenjivim veličinama. Dobivamo z = 4 − x − g .

Svedimo ovaj trostruki integral na niz od tri određena integrala:

.

Izračunavamo najunutarnji integral - nad varijablom z, uzimajući u obzir x i y konstante. Dobivamo:

.

Računamo prosječni integral – preko varijable g. Dobivamo:

.

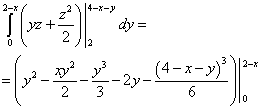Izračunavamo najudaljeniji integral - preko varijable x i konačno nalazimo ovaj trostruki integral:

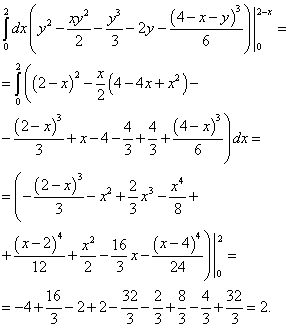
Odgovor: Ovaj trostruki integral jednak je 2.

Promjena varijabli u trostrukom integralu i cilindričnim koordinatama

Ako je projekcija integracijske domene na bilo koju od koordinatnih ravnina kružnica ili dio kružnice, tada je trostruki integral lakše izračunati prelaskom na cilindrične koordinate. Cilindrični koordinatni sustav je generalizacija polarni koordinatni sustav svemiru. U cilindričnom koordinatnom sustavu točka M karakteriziraju tri veličine ( r, φ , z), Gdje r- udaljenost od ishodišta do projekcije N bodova M do aviona xOy, φ - kut između vektora NA i pozitivnog smjera osi Vol, z- nanesite točku M(slika ispod).

Pravokutne koordinate x, g, z s cilindričnim koordinatama r, φ , z povezati formule

x = r cos φ ,

g = r grijeh φ ,

z = z .

Kako biste prešli na cilindrične koordinate u trostrukom integralu, trebate izraziti integrand kao funkciju varijabli r, φ , z:

Odnosno, prijelaz s pravokutnih na cilindrične koordinate provodi se na sljedeći način:

Trostruki integral u cilindričnim koordinatama izračunava se na isti način kao u kartezijevim pravokutnim koordinatama, transformirajući ga u niz od tri određena integrala:

Primjer 8. Izračunajte trostruki integral

prijelaz u cilindrične koordinate, gdje V- područje ograničeno površinama i.

Riješenje. Budući da područje V do aviona xOy se projicira u krug, zatim koordinata φ varira od 0 do 2 π , i koordinata r- od r=0 do r=1. Konstantna vrijednost u prostoru odgovara cilindru. Uzimajući u obzir presjek ovog cilindra s regijom V, dobivamo promjenu ordinate z iz z = r do z= 1. Prijeđimo na cilindrične koordinate i dobijemo.

Krivolinijski integral 1. vrste

1. Duljina krivulje

Ako je integrand funkcije f(x, y, z) ? 1, tada iz definicije krivocrtnog integrala 1. vrste dobivamo da je u ovom slučaju jednaka duljini krivulja po kojoj se vrši integracija:

2. Krivulja mase

Pod pretpostavkom da je integrand funkcija? (x, y, z) određuje gustoću svake točke krivulje, masu krivulje nalazimo pomoću formule

Primjer 23.

Odredite masu krivulje s linearnom gustoćom zadanom u polarnim koordinatama jednadžbom

Koristimo formulu (86):

3. Nalazimo momente krivulje l, razmišljajući na isti način kao u slučaju ravnog područja:

Statički momenti ravninske krivulje l u odnosu na osi Ox i Oy;

• - (88)
• - moment tromosti prostorne krivulje u odnosu na ishodište;

• -momenti tromosti krivulje u odnosu na koordinatne osi.
• 4. Koordinate središta mase krivulje izračunavaju se pomoću formula

Krivolinijski integral 2. vrste

odnosno krivolinijski integral 2. vrste.

Primjer 24.

Izračunajte rad sile koja djeluje na točku koja se giba pravocrtno od točke A(2; 1; 0) do točke B(-3; 2; 1).

Parametarske jednadžbe pravca AB imaju oblik:

U ovom slučaju je dx = -5dt, dy = dt, dz = dt.

• 4. Površinski integral 1. vrste
• 1. Površina zakrivljene površine, čija je jednadžba

z = f(x, y), može se naći u obliku:

• (? - projekcija S na Oxy ravninu).
• 2. Površinska masa

Primjer 25.

Odredite masu površine S: x2 + y2 + z2 = 4, s površinskom gustoćom.

Definirajmo površinu S eksplicitno: i pronađimo dS:

Ploha S je dio sfere polumjera 2 sa središtem u ishodištu, izrezan ravninom. Nađimo projekciju te plohe na koordinatnu ravninu Oxy. Sjecište sfere i ravnine je kružnica, odnosno x2 + y2 = 1. Prema tome, projekcija S na Oxy ravninu je kružnica jediničnog polumjera sa središtem u ishodištu.

Izračunajmo masu površine u polarnim koordinatama:

3. Trenuci:

Statički momenti površine u odnosu na koordinatne ravnine Oxy, Oxz, Oyz;

Momenti tromosti površine u odnosu na koordinatne osi;

Momenti tromosti površine u odnosu na koordinatne ravnine;

• - moment tromosti površine u odnosu na ishodište.
• 4. Koordinate središta mase površine:

Komentar. Budući da se formule koje specificiraju vrijednosti geometrijskih i fizikalnih veličina pomoću integrala izvode istim tehnikama za integrale svih tipova koji se razmatraju, njihovo detaljno izvođenje dano je tek na početku poglavlja. Ako želite, možete izvesti slično zaključivanje za trostruke, krivocrtne i površinske integrale i dobiti sve formule bez detaljnog izvođenja.

Predavanje 7. Površinski integrali.

Problem površinske mase.

Problem površinske mase dovodi nas do površinski integral 1. vrsta, kao što nas je problem mase krivulje doveo do krivocrtnog integrala prve vrste.

Neka je površinska gustoća f(x, y, z) određena u svakoj točki komadično glatke površine s.

1. Uvedimo particiju s u elementarna područja Ds i - elemente particije tako da nemaju zajedničkih unutarnje točke (uvjet A).

2. Označite točke M i na elementima pregrade Ds i . Izračunamo f (M i) = f (x i, y i, z i) i smatramo gustoću konstantnom i jednakom f (M i) na cijelom pregradnom elementu Ds i. Izračunajmo masu pregradne ćelije približno kao f ( M i) Ds i. Približno izračunajmo masu površine s zbrajanjem masa ćelija (sastavljanjem integralnog zbroja). U integralnom zbroju, ovo je površina jedinične ćelije. Ovdje se, kao i prije, tradicionalno koristi ista oznaka za samu elementarnu ćeliju i njezino područje.

3. Pročišćavamo particiju i idemo do limita u integralnom zbroju pod uvjetom (stanjeB) . Dobivamo površinski integral prve vrste, koja je jednaka masi površine (osim ako je f(M i)>0 na površini).

= .

Teorem egzistencije. Neka funkcija kontinuirana je na komadićima glatkoj omeđenoj površini. Tada površinski integral prve vrste postoji kao limit integralnih suma.

= .

Komentar. Integral (kao granica integralnih suma) ne ovisi o:

1) o izboru podjele površine (sve dok je zadovoljen uvjet A),

2) od izbora označenih točaka na elementima pregrade,

3) o načinu dotjerivanja particije (sve dok je zadovoljen uvjet B).

Svojstva površinskog integrala prve vrste.

(po formulaciji i dokazu slični su svojstvima prethodno razmatranih integrala prve vrste).

1) Linearnost.

2) Aditivnost

3) - površina.

4) Ako je , tada (ako tada),

5) Teorem o procjeni. Ako , To ,

6) Teorem o srednjoj vrijednosti. Neka funkcija kontinuirana je na komadićima glatkoj omeđenoj površini. Tada postoji točka C na površini takva da

Dokaz. Prva četiri svojstva dokazuju se slično sličnim svojstvima dvostrukih, trostrukih integrala i krivocrtnog integrala prve vrste (ispisivanjem relacija u integralnim zbrojevima i prelaskom na limes). Drugo svojstvo koristi mogućnost podjele površine na dva dijela tako da niti jedan element pregrade ne sadrži granične točke tih dijelova kao svoje unutarnje točke.

Teorem procjene slijedi iz svojstava 3, 4.

Teorem srednje vrijednosti, kao i prije, koristi Weierstrassov i Bolzano-Cauchyjev teorem za funkcije koje su kontinuirane na zatvorenim ograničenim skupovima.

Izračun površinskog integrala prve vrste.

Prethodno smo u drugom predavanju pomoću dvostrukog integrala izračunali površinu, odnosno integral smo sveli na dvostruki integral. Sada moramo smanjiti integral dvostrukom integralu. Ponovno ponavljajući iste izračune s jedinom razlikom što ispod integrala stoji funkcija, dobivamo sličnu formulu za površinu određenu relacijom

=.

Ako je površina dana jednadžbom, dobivamo formulu na potpuno isti način

= . Ovdje moramo uzeti u obzir da točka (x, y, z) leži na površini.

Primjer. Odredite masu površine homogene hemisfere , z>0 s konstantnom površinskom gustoćom W.

Označimo D - krug – projekciju hemisfere na OXY ravninu.

=.

Površinski integral druge vrste.

Površina se zove orijentiran, ako u svakoj njegovoj točki postoji vektor normale na , kontinuirani je vektor – funkcija na .

Površina se zove jednostrano, ako hodajući po površini duž konture g, vektor normale promijeni smjer u suprotan.

Površina se zove bilateralni, ako pri hodu po površini po konturi g vektor normale ne mijenja smjer.

Primjer jednostrane plohe je Möbiusova petlja; primjeri dvostrane plohe su ravnina, sfera, hiperboloidi itd.

Problem strujanja tekućine kroz površinu.

Protok tekućine kroz površinu je količina tekućine koja protječe kroz površinu u jedinici vremena.

Neka je na elementu površine platforme u nekoj točki M nacrtan vektor pomaka čestice fluida kroz platformu u jedinici vremena. Pretpostavljamo da je za sve točke pomak jednak po veličini i smjeru. Protok fluida može se izračunati kao volumen nagnutog (u smjeru vektora pomaka) paralelopipeda izgrađenog na . Ovaj volumen je jednak , gdje je jedinični vektor normale na površinu. Tada je protok tekućine jednak P =

Ovdje smo izračunali diferencijal protoka, a zatim integrirali po cijeloj površini - to je metoda diferencijala pri konstruiranju integrala.

Integral možete konstruirati koristeći metodu integralnih suma, kao što smo to obično činili.

Uvedimo podjelu regije na elemente tako da susjedni elementi nemaju zajedničke unutarnje točke ( uvjet A),

Na elementima pregrade označimo točku M. Uz pretpostavku da je kretanje čestica fluida konstantno na elementu i jednako (M), aproksimativno izračunamo protok kroz element pregrade i zbrojimo ga po elementima, dobivamo integralni zbroj .

Pročistimo particiju pod uvjetom ( uvjet B) i idu do granice, dobivajući površinski integral druge vrste

.

Po izgledu, ovo je površinski integral prve vrste, ima ista svojstva kao površinski integral prve vrste, ali ima i svojstvo orijentacije. Integral po vanjskoj strani plohe razlikuje se predznakom od integrala po iznutra površine, budući da su na različitim stranama površine normale u istoj točki usmjerene duž jedne ravne crte u različitim smjerovima.

1) Integral po površini prve vrste

2) Posebna vektorska polja

3) Stokesov teorem

4) Potencijalno polje

Književnost

vektor potencijal polja integral

Integral nad plohom prve vrste

Fizički problemi koji dovode do površinskog integrala mogu biti dvije vrste:

1) nije u vezi sa smjerom normale na površinu

Na primjer, problemi s pronalaženjem mase ili naboja raspoređenog po površini:

2) - ovisi o smjeru normale - problem nalaženja strujanja fluida u smjeru normale.

dano: -kontinuirana funkcija na

Površinski:

1) Podijelite površinu na n dijelova

2) Uzmi bod

3) Izračunajte -gustoću

Stoga

gdje je D projekcija na ravninu XOY

Primjer. Gustoćom odredite masu raspoređenu na površini

Posebna vektorska polja.

1. Divergencija.
2. Solenoidna polja. Svojstva.

1. Definicija divergencije

Ostrogradsky-Gaussov teorem

Pronađite tok vektora usmjeren na negativna strana os Ox, odsječena ravninom kroz dio paraboloida

Definicija. Vektorsko polje za sve čije točke nazivamo solenoidnim u domeni. Solenoidno polje je slobodno od izvora.

Svojstva solenoidnih polja.

1. Ako je solenoidno polje zadano u jednostavno povezanom području, tada je tok vektora kroz bilo koju zatvorenu površinu tog područja jednak nuli.

Neka je solenoidno polje u jednostavno povezanom području. Tada vektorski tok kroz bilo koju plohu obuhvaćenu zadanom konturom G ne ovisi o vrsti te plohe, već samo o konturi.

Primijenimo Ostrogradsky-Gaussov teorem.

1. Svojstva vektorske cijevi.

Definicija. Vektorska linija je linija u svakoj točki u kojoj se smjer tangente na nju podudara sa smjerom polja.

vektorska linija.

Uzmite zatvorenu konturu u polju i nacrtajte vektorske linije kroz njene točke

Bilo koja druga vektorska linija koja prolazi kroz konturne točke prolazi ili unutar cijevi ili izvan cijevi.

U slučaju strujanja fluida, vektorska cijev je dio prostora koji je ispunjen volumenom fluida dok se kreće.

Intenzitet vektorske cijevi zove se protok polja poprečni presjek ova cijev.

1. Ako je polje solenoidno u jednostavno povezanom području

   Tada je intenzitet vektorske cijevi konstantan duž cijele cijevi.

Dokaz:

Bočna površina, vektorske linije su okomite. Prema tome (normala na je normala polja, tj.)

i imaju suprotne smjerove.

Protok kroz bilo koju transverzalu je jednak ako je solenoidalna.

1. U solenoidnom polju

   vektorske linije ne mogu počinjati niti završavati unutar polja. Ili su zatvorene, imaju krajeve na granici polja ili imaju beskonačne grane.

Dokaz:

Prema svojstvu 3, intenzitet cijevi je isti, iako je presjek u točki M jednak nuli, u T M. To je nemoguće jer kontinuirano u bilo kojoj točki.

Stokesov teorem.

Vrtlog. Rotor.

Cirkulacija.

1. Stokesov teorem

Pojam rotora ili vrtloga usko je povezan s pojmom cirkulacije. Lokalna karakteristika polja povezana s vrtložnošću je rotor.

Ravno polje.

S područje iznutra

polje brzine tekućine koja teče

U polje postavljamo kotač s lopaticama, po dužini. Čestice tekućine koje djeluju na te lopatice stvorit će okretni moment čije će ukupno djelovanje uzrokovati rotaciju kotača oko svoje osi. Rotacijsko djelovanje polja brzine tekućine u bilo kojoj točki M karakterizirat će se na tangenti na kružnicu, tj. skalarni proizvod. Zbrajanje rotacijskih učinaka tekućine duž cijele konture kotača dovest će do koncepta vektorske cirkulacije =

On će odrediti kutnu brzinu vrtnje kotača, a predznak cirkulacije pokazat će u kojem se smjeru kotač okreće u odnosu na odabrani smjer.

Kruženje bilo kojeg polja određuje njegovu rotacijsku sposobnost oko sebe ovaj smjer i karakterizira vrtložnost polja u ovom smjeru.

Što je manja, veća je cirkulacija, veća je vrtložnost.

Maksimalni vrtlog ako

Gustoća cirkulacije u točki.

Ako je polje prostorno, tada možemo govoriti o vrtložnosti u pravcu.

Vrtložnost u smjeru.

Definicija: u točki se naziva vektor čija je projekcija na svaki smjer jednaka granici omjera cirkulacije vektorskog polja duž konture u ravnom području okomitom na ovaj smjer prema površini S ovog područja , kada je, a regija je kontrahirana u točki, tj.

Kontura koja leži u ravnini okomitoj na vektor

Stokesov teorem. -površinska jednostavno povezana regija. - komadno glatka kontura u, - komadno glatka površina prevučena.