Integration of fractionally rational functions of type 4. Integration of a fractional-rational function. Method of undetermined coefficients. Educational institution "Belarusian State

“A mathematician, just like an artist or poet, creates patterns. And if his patterns are more stable, it is only because they are composed of ideas... The patterns of a mathematician, just like the patterns of an artist or a poet, must be beautiful; Ideas, just like colors or words, must correspond to each other. Beauty is the first requirement: there is no place in the world for ugly mathematics».

G.H.Hardy

In the first chapter it was noted that there are primitives quite simple functions, which can no longer be expressed through elementary functions. In this regard, those classes of functions about which we can accurately say that their antiderivatives are elementary functions acquire enormous practical importance. This class of functions includes rational functions, representing the ratio of two algebraic polynomials. Many problems lead to the integration of rational fractions. Therefore, it is very important to be able to integrate such functions.

2.1.1. Fractional rational functions

Rational fraction(or fractional rational function) is called the relation of two algebraic polynomials:

where and are polynomials.

Let us remind you that polynomial (polynomial, whole rational function ) nth degree called a function of the form

Where – real numbers. For example,

– polynomial of the first degree;

– polynomial of the fourth degree, etc.

The rational fraction (2.1.1) is called correct, if the degree is lower than the degree , i.e. n<m, otherwise the fraction is called wrong.

Any improper fraction can be represented as the sum of a polynomial (the whole part) and a proper fraction (the fractional part). The separation of the whole and fractional parts of an improper fraction can be done according to the rule for dividing polynomials with a “corner”.

Example 2.1.1. Identify the whole and fractional parts of the following improper rational fractions:

A) 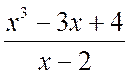, b) .

Solution . a) Using the “corner” division algorithm, we get

Thus, we get

.

b) Here we also use the “corner” division algorithm:

As a result, we get

.

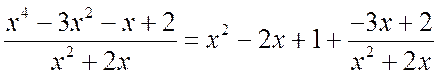Let's summarize. In the general case, the indefinite integral of a rational fraction can be represented as the sum of the integrals of the polynomial and the proper rational fraction. Finding antiderivatives of polynomials is not difficult. Therefore, in what follows we will mainly consider proper rational fractions.

2.1.2. The simplest rational fractions and their integration

Among proper rational fractions, there are four types, which are classified as the simplest (elementary) rational fractions:

where is an integer, , i.e. quadratic trinomial has no real roots.

Integrating simple fractions of the 1st and 2nd types does not present any great difficulties:

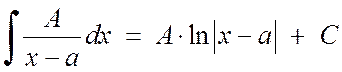, (2.1.3)

. (2.1.4)

Let us now consider the integration of simple fractions of the 3rd type, but we will not consider fractions of the 4th type.

Let's start with integrals of the form

.

This integral is usually calculated by isolating the perfect square of the denominator. The result is a table integral of the following form

or .

Example 2.1.2. Find the integrals:

A) , b) .

Solution . a) Select a complete square from a quadratic trinomial:

From here we find

b) By isolating a complete square from a quadratic trinomial, we obtain:

Thus,

.

To find the integral

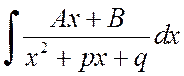
you can isolate the derivative of the denominator in the numerator and expand the integral into the sum of two integrals: the first of them by substitution comes down to appearance

,

and the second - to the one discussed above.

Example 2.1.3. Find the integrals:

.

Solution . notice, that 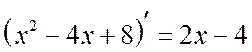. Let us isolate the derivative of the denominator in the numerator:

The first integral is calculated using the substitution :

In the second integral, we select the perfect square in the denominator

Finally, we get

2.1.3. Proper rational fraction expansion
for the sum of simple fractions

Any proper rational fraction can be represented in a unique way as a sum of simple fractions. To do this, the denominator must be factorized. From higher algebra it is known that every polynomial with real coefficients

Integration of rational functions Fractional - rational function The simplest rational fractions Decomposition of a rational fraction into simple fractions Integration of simple fractions General rule for the integration of rational fractions

polynomial of degree n. Fractional - rational function A fractional - rational function is a function equal to the ratio of two polynomials: A rational fraction is called proper if the degree of the numerator is less than the degree of the denominator, that is, m< n , в противном случае дробь называется неправильной. многочлен степени m Всякую неправильную рациональную дробь можно, путем деления числителя на знаменатель, представить в виде суммы многочлена L(x) и правильной рациональной дроби:)()()(x. Q x. P xf n m)()()(x. Q x. R x. L x. Q x. P

Fractional - rational function Reduce an improper fraction to the correct form: 2 95 4 x xx 95 4 xx 2 x 3 x 34 2 xx 952 3 xx 2 2 x 23 42 xx 954 2 xx x 4 xx 84 2 93 x 3 63 x 15 2 95 4 x xx 342 23 xxx 2 15 x

Simplest rational fractions Proper rational fractions of the form: They are called simplest rational fractions of types. ax A); 2(Nkk ax A k)04(2 2 qp qpxx NMx); 2; 04(2 2 Nkkqp qpxx NMx k V V,

Decomposition of a rational fraction into simple fractions Theorem: Any proper rational fraction, the denominator of which is factorized: can be represented, moreover, in a unique way in the form of a sum of simple fractions: s k qxpxxxxxx. Q)()()(22 2 11 2 21)()(x. Q x. P 1 xx A k k xx B)()(2 2 2 1 11 2 qxpx DCx 2 22 22 2 11)(qxpx Nx. M s ss qxpx Nx. M)(

Decomposition of a rational fraction into simple fractions Let us explain the formulation of the theorem using the following examples: To find the uncertain coefficients A, B, C, D..., two methods are used: the method of comparing coefficients and the method of partial values ​​of a variable. Let's look at the first method using an example. 3 2)3)(2(4 xx x 2 x A 3 3 2 21)3()3(3 x B x B 1 2 x DCx 22 22 2 11)1(1 xx Nx. M)1(3 22 3 xx x 2 21 x A 22 2)1)(4(987 xxx xx 4 x

Decomposition of a rational fraction into simple fractions Present the fraction as a sum of simple fractions: Let's bring the simplest fractions to a common denominator Equate the numerators of the resulting and original fractions Equate the coefficients at the same powers x)52)(1(332 2 2 xxx xx 1 x A 52 2 xx CBx )52)(1()1)(()52(2 2 xxx x. CBxxx. A 33252 222 xx. CBx. Cx. Bx. AAx. Ax 35 32 2 0 1 2 CAx BAx 2 3 1 C B A 52 23 1 1 2 xx x x

Integration of the simplest fractions Let's find the integrals of the simplest rational fractions: Let's look at the integration of type 3 fractions using an example. dx ax A k dx qpxx NMx 2 ax axd A)(Cax. Aln)(axdax. A k C k ax. A k

Integration of simple fractionsdx xx x 102 13 2 dx xx x 9)12(13 2 dx x x 9)1(13 2 dtdx tx tx 1 1 dt t t 9 1)1(3 2 dt t t 9 23 2 9 322 t dtt 9 9 2 3 2 2 t td 33 2 t arctg.C t arctgt 33 2 9 ln 2 32 C x arctgxx 3 1 3 2 102 ln

Integration of simple fractions An integral of this type using substitution: is reduced to the sum of two integrals: The first integral is calculated by introducing t under the differential sign. The second integral is calculated using the recurrence formula: dx qpxx NMx k 2 V t p x 2 kk at dt N at dtt M 22122 1221222))(1(222 321 kkkk atk t k k aat dt

Integration of simple fractions a = 1; k = 3 323)1(t dt tarctg t dt 1 21)1)(12(2222 322 1 21222 t t t dt)1(22 1 2 t t tarctg 2223)1)(13(2232 332 t t C t t tarctg 222)1 (4)1(

General rule for integrating rational fractions If the fraction is improper, then represent it as the sum of a polynomial and a proper fraction. Having factorized the denominator of a proper rational fraction, represent it as a sum of simple fractions with indefinite coefficients. Find indefinite coefficients by the method of comparing coefficients or by the method of partial values ​​of a variable. Integrate the polynomial and the resulting sum of simple fractions.

Example Let's put the fraction in the correct form. dx xxx 23 35 2 442 35 xxxxxx 23 2 2 x 345 2 xxx 442 34 xxx x 2 234 242 xxx 4425 23 xxx xxx 23 35 2 442 xxx xx xx 23 2 2 2 48 52 5 xxx 5105 23 48 2 xx

Example Let's factorize the denominator of a proper fraction Let's represent the fraction as a sum of simple fractions Let's find the undetermined coefficients using the method of partial values ​​of the variable xxx xx 23 2 2 48 2 2)1(48 xx xx 2)1(1 x C x B x A 2 2)1 ()1(xx Cxx. Bxx. A 48)1()1(22 xx. Cxx. Bxx. A 5241 31 40 CBAx Cx Ax 3 12 4 C B A xxx xx 23 2 2 48 2)1(3 1 124 xxx

Example dx xx 2 2)1(3 1 124 52 2 2)1(3 1 12452 x dx dxxdxdxx C x xxxx x 1 3 1 ln 12 ln

A rational function is a fraction of the form , the numerator and denominator of which are polynomials or products of polynomials.

Example 1. Step 2.

.

We multiply the undetermined coefficients by polynomials that are not in this individual fraction, but which are in other resulting fractions:

We open the brackets and equate the numerator of the original integrand to the resulting expression:

In both sides of the equality, we look for terms with the same powers of x and compose a system of equations from them:

.

We cancel all the x’s and get an equivalent system of equations:

.

Thus, the final expansion of the integrand into a sum of simple fractions is:

.

Example 2. Step 2. At step 1, we obtained the following decomposition of the original fraction into the sum of simple fractions with undetermined coefficients in the numerators:

.

Now we begin to look for uncertain coefficients. To do this, we equate the numerator of the original fraction in the function expression to the numerator of the expression obtained after reducing the sum of fractions to a common denominator:

Now you need to create and solve a system of equations. To do this, we equate the coefficients of the variable to the corresponding degree in the numerator of the original expression of the function and similar coefficients in the expression obtained at the previous step:

We solve the resulting system:

So, from here

.

Example 3. Step 2. At step 1, we obtained the following decomposition of the original fraction into the sum of simple fractions with undetermined coefficients in the numerators:

We begin to look for uncertain coefficients. To do this, we equate the numerator of the original fraction in the function expression to the numerator of the expression obtained after reducing the sum of fractions to a common denominator:

As in previous examples, we compose a system of equations:

We reduce the x's and get an equivalent system of equations:

Solving the system, we obtain the following values ​​of the uncertain coefficients:

We obtain the final decomposition of the integrand into the sum of simple fractions:

.

Example 4. Step 2. At step 1, we obtained the following decomposition of the original fraction into the sum of simple fractions with undetermined coefficients in the numerators:

.

We already know from previous examples how to equate the numerator of the original fraction with the expression in the numerator obtained after decomposing the fraction into the sum of simple fractions and bringing this sum to a common denominator. Therefore, just for control purposes, we present the resulting system of equations:

Solving the system, we obtain the following values ​​of the uncertain coefficients:

We obtain the final decomposition of the integrand into the sum of simple fractions:

Example 5. Step 2. At step 1, we obtained the following decomposition of the original fraction into the sum of simple fractions with undetermined coefficients in the numerators:

.

We independently reduce this sum to a common denominator, equating the numerator of this expression to the numerator of the original fraction. The result should be the following system of equations:

Solving the system, we obtain the following values ​​of the uncertain coefficients:

.

We obtain the final decomposition of the integrand into the sum of simple fractions:

.

Example 6. Step 2. At step 1, we obtained the following decomposition of the original fraction into the sum of simple fractions with undetermined coefficients in the numerators:

We perform the same actions with this amount as in the previous examples. The result should be the following system of equations:

Solving the system, we obtain the following values ​​of the uncertain coefficients:

.

We obtain the final decomposition of the integrand into the sum of simple fractions:

.

Example 7. Step 2. At step 1, we obtained the following decomposition of the original fraction into the sum of simple fractions with undetermined coefficients in the numerators:

.

After certain actions with the resulting amount, the following system of equations should be obtained:

Solving the system, we obtain the following values ​​of the uncertain coefficients:

We obtain the final decomposition of the integrand into the sum of simple fractions:

.

Example 8. Step 2. At step 1, we obtained the following decomposition of the original fraction into the sum of simple fractions with undetermined coefficients in the numerators:

.

Let's make some changes to the actions that have already been brought to automaticity to obtain a system of equations. There is an artificial technique that in some cases helps to avoid unnecessary calculations. Bringing the sum of fractions to a common denominator, we obtain and equating the numerator of this expression to the numerator of the original fraction, we obtain.