Find the smallest value of the function examples. The largest and smallest value of a function on a segment. What will we study

A miniature and rather simple task of the kind that serves as a lifeline for a floating student. In nature, the sleepy realm of mid-July, so it's time to settle down with a laptop on the beach. Early in the morning, a sunbeam of theory began to play in order to soon focus on practice, which, despite its declared lightness, contains glass fragments in the sand. In this regard, I recommend conscientiously consider a few examples of this page. To solve practical tasks, you need to be able to find derivatives and understand the material of the article Intervals of monotonicity and extrema of a function.

First, briefly about the main thing. In a lesson about function continuity I gave the definition of continuity at a point and continuity on an interval. The exemplary behavior of a function on a segment is formulated in a similar way. A function is continuous on a segment if:

1) it is continuous on the interval ;
2) continuous at a point on right and at the point left.

The second paragraph deals with the so-called unilateral continuity functions at a point. There are several approaches to its definition, but I will stick to the line started earlier:

The function is continuous at a point on right, if it is defined at a given point and its right-hand limit coincides with the value of the function at a given point: . It is continuous at the point left, if defined at a given point and its left-hand limit is equal to the value at that point:

Imagine that the green dots are the nails on which the magic rubber band is attached:

Mentally take the red line in your hands. Obviously, no matter how far we stretch the graph up and down (along the axis), the function will still remain limited- a hedge above, a hedge below, and our product grazes in a paddock. In this way, a function continuous on a segment is bounded on it. In the course of mathematical analysis, this seemingly simple fact is stated and rigorously proved Weierstrass' first theorem.… Many people are annoyed that elementary statements are tediously substantiated in mathematics, but this has an important meaning. Suppose a certain inhabitant of the terry Middle Ages pulled the graph into the sky beyond the limits of visibility, this was inserted. Before the invention of the telescope, the limited function in space was not at all obvious! Indeed, how do you know what awaits us beyond the horizon? After all, once the Earth was considered flat, so today even ordinary teleportation requires proof =)

According to second Weierstrass theorem, continuous on the segmentfunction reaches its exact top edge and his exact bottom edge .

The number is also called the maximum value of the function on the segment and denoted by , and the number - the minimum value of the function on the segment with notice .

In our case:

Note : in theory, records are common .

Roughly speaking, the largest value is located where the highest point of the graph, and the smallest - where the lowest point.

Important! As already pointed out in the article on extrema of the function, the largest value of the function And smallest function value – NOT THE SAME, what function maximum And function minimum. So, in this example, the number is the minimum of the function, but not the minimum value.

By the way, what happens outside the segment? Yes, even the flood, in the context of the problem under consideration, this does not interest us at all. The task involves only finding two numbers and that's it!

Moreover, the solution is purely analytical, therefore, no need to draw!

The algorithm lies on the surface and suggests itself from the above figure:

1) Find the function values ​​in critical points, that belong to this segment.

Catch one more goodie: there is no need to check a sufficient condition for an extremum, since, as just shown, the presence of a minimum or maximum not yet guaranteed what is the minimum or maximum value. The demonstration function reaches its maximum and, by the will of fate, the same number is the largest value of the function on the interval . But, of course, such a coincidence does not always take place.

So, at the first step, it is faster and easier to calculate the values ​​of the function at critical points belonging to the segment, without bothering whether they have extrema or not.

2) We calculate the values ​​of the function at the ends of the segment.

3) Among the values ​​​​of the function found in the 1st and 2nd paragraphs, select the smallest and largest number, write down the answer.

We sit on the shore of the blue sea and hit the heels in shallow water:

Example 1

Find the largest and smallest values ​​of a function on a segment

Solution:
1) Calculate the values ​​of the function at critical points belonging to this segment:

Let us calculate the value of the function at the second critical point:

2) Calculate the values ​​of the function at the ends of the segment:

3) "Bold" results were obtained with exponentials and logarithms, which significantly complicates their comparison. For this reason, we will arm ourselves with a calculator or Excel and calculate the approximate values, not forgetting that:

Now everything is clear.

Answer:

Fractional-rational instance for independent solution:

Example 6

Find the maximum and minimum values ​​of a function on a segment

Let the function y=f(X) continuous on the interval [ a, b]. As is known, such a function reaches its maximum and minimum values ​​on this segment. The function can take these values ​​either at an interior point of the segment [ a, b], or on the boundary of the segment.

To find the largest and smallest values ​​of a function on the interval [ a, b] necessary:

1) find the critical points of the function in the interval ( a, b);

2) calculate the values ​​of the function at the found critical points;

3) calculate the values ​​of the function at the ends of the segment, that is, for x=but and x = b;

4) from all the calculated values ​​of the function, choose the largest and smallest.

Example. Find the largest and smallest values ​​of a function

on the segment.

Finding critical points:

These points lie inside the segment ; y(1) = ‒ 3; y(2) = ‒ 4; y(0) = ‒ 8; y(3) = 1;

at the point x= 3 and at the point x= 0.

Investigation of a function for convexity and an inflection point.

Function y = f (x) called convexup in between (a, b) , if its graph lies under a tangent drawn at any point of this interval, and is called convex down (concave) if its graph lies above the tangent.

The point at the transition through which the convexity is replaced by concavity or vice versa is called inflection point.

Algorithm for studying for convexity and inflection point:

1. Find the critical points of the second kind, that is, the points at which the second derivative is equal to zero or does not exist.

2. Put critical points on the number line, breaking it into intervals. Find the sign of the second derivative on each interval; if , then the function is convex upwards, if, then the function is convex downwards.

3. If, when passing through a critical point of the second kind, it changes sign and at this point the second derivative is equal to zero, then this point is the abscissa of the inflection point. Find its ordinate.

Asymptotes of the graph of a function. Investigation of a function into asymptotes.

Definition. The asymptote of the graph of a function is called straight, which has the property that the distance from any point of the graph to this line tends to zero with an unlimited removal of the graph point from the origin.

There are three types of asymptotes: vertical, horizontal and inclined.

Definition. Direct called vertical asymptote function graph y = f(x), if at least one of the one-sided limits of the function at this point is equal to infinity, that is

where is the discontinuity point of the function, that is, it does not belong to the domain of definition.

Example.

D( y) = (‒ ∞; 2) (2; + ∞)

x= 2 - breaking point.

Definition. Straight y=A called horizontal asymptote function graph y = f(x) at , if

Example.

x
y

Definition. Straight y=kx +b (k≠ 0) is called oblique asymptote function graph y = f(x) at , where

General scheme for the study of functions and plotting.

Function research algorithmy = f(x) :

1. Find the domain of the function D (y).

2. Find (if possible) the points of intersection of the graph with the coordinate axes (with x= 0 and at y = 0).

3. Investigate for even and odd functions ( y (‒ x) = y (x) ‒ parity; y(‒ x) = ‒ y (x) ‒ odd).

4. Find the asymptotes of the graph of the function.

5. Find intervals of monotonicity of the function.

6. Find the extrema of the function.

7. Find the intervals of convexity (concavity) and inflection points of the graph of the function.

8. On the basis of the conducted research, construct a graph of the function.

Example. Investigate the function and plot its graph.

1) D (y) =

x= 4 - breaking point.

2) When x = 0,

(0; – 5) – point of intersection with oy.

At y = 0,

3) y(‒ x)= general function (neither even nor odd).

4) We investigate for asymptotes.

a) vertical

b) horizontal

c) find oblique asymptotes where

‒oblique asymptote equation

5) In this equation, it is not required to find intervals of monotonicity of the function.

6)

These critical points partition the entire domain of the function on the interval (˗∞; ˗2), (˗2; 4), (4; 10) and (10; +∞). It is convenient to present the obtained results in the form of the following table.

How to find the largest and smallest values ​​of a function on a segment?

For this we follow the well-known algorithm:

1 . We find ODZ functions.

2 . Finding the derivative of a function

3 . Equate the derivative to zero

4 . We find the intervals on which the derivative retains its sign, and from them we determine the intervals of increase and decrease of the function:

If on the interval I the derivative of the function 0" title="(!LANG:f^(prime)(x)>0">, то функция !} increases over this interval.

If on the interval I the derivative of the function , then the function decreases over this interval.

5 . We find maximum and minimum points of the function.

IN the function maximum point, the derivative changes sign from "+" to "-".

IN minimum point of the functionderivative changes sign from "-" to "+".

6 . We find the value of the function at the ends of the segment,

• then we compare the value of the function at the ends of the segment and at the maximum points, and choose the largest of them if you need to find the largest value of the function
• or we compare the value of the function at the ends of the segment and at the minimum points, and choose the smallest of them if you need to find the smallest value of the function

However, depending on how the function behaves on the interval, this algorithm can be significantly reduced.

Consider the function . The graph of this function looks like this:

Let's consider several examples of solving problems from the Open Task Bank for

one . Task B15 (#26695)

On the cut.

1. The function is defined for all real values ​​of x

Obviously, this equation has no solutions, and the derivative is positive for all values ​​of x. Therefore, the function increases and takes on the largest value at the right end of the interval, that is, at x=0.

Answer: 5.

2 . Task B15 (No. 26702)

Find the largest value of a function on the segment.

1.ODZ function title="(!LANG:x(pi)/2+(pi)k, k(in)(bbZ)">!}

The derivative is zero at , however, at these points it does not change sign:

Therefore, title="(!LANG:3/(cos^2(x))>=3">, значит, title="3/(cos^2(x))-3>=0">, то есть производная при всех допустимых значених х неотрицательна, следовательно, функция !} increases and takes the greatest value at the right end of the interval, at .

To make it clear why the derivative does not change sign, we transform the expression for the derivative as follows:

Title="(!LANG:y^(prime)=3/(cos^2(x))-3=(3-3cos^2(x))/(cos^2(x))=(3sin^2 (x))/(cos^2(x))=3tg^2(x)>=0">!}

Answer: 5.

3 . Task B15 (#26708)

Find the smallest value of the function on the interval .

1. ODZ functions: title="(!LANG:x(pi)/2+(pi)k, k(in)(bbZ)">!}

Let's place the roots of this equation on a trigonometric circle.

The interval contains two numbers: and

Let's put up the signs. To do this, we determine the sign of the derivative at the point x=0: . When passing through the points and the derivative changes sign.

Let's depict the change of signs of the derivative of the function on the coordinate line:

Obviously, the point is a minimum point (where the derivative changes sign from "-" to "+"), and in order to find the smallest value of the function on the segment, you need to compare the function values ​​at the minimum point and at the left end of the segment, .

Lesson on the topic: "Finding the largest and smallest values ​​of a continuous function on a segment"

Additional materials
Dear users, do not forget to leave your comments, feedback, suggestions! All materials are checked by an antivirus program.

Manuals and simulators in the online store "Integral" for grade 10 from 1C
We solve problems in geometry. Interactive construction tasks for grades 7-10
We solve problems in geometry. Interactive tasks for building in space

What will we study:

1. Finding the largest and smallest values ​​according to the graph of the function.
2. Finding the largest and smallest value using the derivative.
3. Algorithm for finding the largest and smallest values ​​of a continuous function y=f(x) on the segment .
4. The largest and smallest value of a function on an open interval.
5. Examples.

Finding the largest and smallest value from the graph of a function

Guys, we have found the largest and smallest values ​​of the function before. We looked at the graph of a function and concluded where the function reaches its maximum value, and where it reaches its minimum.
Let's repeat:

The graph of our function shows that the largest value is reached at the point x= 1, it is equal to 2. The smallest value is reached at the point x= -1, and it is equal to -2. In this way, it is quite easy to find the largest and smallest values, but it is not always possible to plot a function graph.

Finding the largest and smallest value using the derivative

Guys, what do you think, how can you find the largest and smallest value using the derivative?

The answer can be found in the topic extrema of the function. There you and I found the maximum and minimum points, aren't the terms similar. However, one should not confuse the maximum and minimum values ​​with the maximum and minimum of a function, these are different concepts.

So let's introduce the rules:
a) If a function is continuous on an interval, then it reaches its maximum and minimum values ​​on this interval.
b) The function can reach the maximum and minimum values ​​both at the ends of the segments and inside it. Let's look at this point in more detail.

In figure a, the function reaches its maximum and minimum values ​​at the ends of the segments.
In figure b, the function reaches its maximum and minimum values ​​inside the interval . In figure c, the minimum point is inside the segment, and the maximum point is at the end of the segment, at point b.
c) If the largest and smallest values ​​are reached inside the segment, then only at stationary or critical points.

Algorithm for finding the largest and smallest values ​​of a continuous function y= f(x) on a segment

• Find the derivative f "(x).
• Find stationary and critical points inside the segment .
• Calculate the value of the function at stationary and critical points, as well as at f(a) and f(b). Choose the smallest and largest values, these will be the points of the smallest and largest values ​​of the function.

The largest and smallest value of a function on an open interval

Guys, how to find the largest and smallest value of a function on an open interval? To do this, we use an important theorem, which is proved in the course of higher mathematics.

Theorem. Let the function y= f(x) be continuous on the interval x, and have inside this interval the only stationary or critical point x= x0, then:
a) if x= x0 is the maximum point, then y is max. = f(x0).
b) if x= x0 is the minimum point, then y min. = f(x0).

Example

Find the largest and smallest value of the function y= $\frac(x^3)(3)$ + 2x 2 + 4x - 5 on the segment
a) [-9;-1], b) [-3; 3], c) .
Solution: Find the derivative: y "= x 2 + 4x + 4.
The derivative exists on the entire domain of definition, then we need to find stationary points.
y"= 0, with x= -2.
Further calculations will be carried out for the required segments.
a) Find the values ​​of the function at the ends of the segment and at the stationary point.
Then y nam. = -122, at x= -9; y max. = y = -7$\frac(1)(3)$, for x= -1.
b) Find the values ​​of the function at the ends of the segment and at the stationary point. The largest and smallest value is reached at the ends of the segment.
Then y nam. = -8, at x= -3, y max. = 34, at x= 3.
c) The stationary point does not fall on our segment, we find the values ​​at the ends of the segment.
Then y nam. = 34, at x= 3, y max. = 436, at x= 9.

Example

Find the largest and smallest value of the function y= x 2 - 3x + 5 + |1-x| on the segment.
Solution: Expand the module and transform our function:
y= x 2 - 3x + 5 + 1 - x, for x ≤ 1.
y= x 2 - 3x + 5 - 1 + x, for x ≥ 1.

Then our function will take the form:
\begin(equation*)f(x)= \begin(cases) x^2 - 4x + 6,\quad if\quad x ≤ 1 \\ x^2 - 2x + 4,\quad if\quad x ≥ 1 \end(cases) \end(equation*) Find critical points: \begin(equation*)f"(x)= \begin(cases) 2x - 4,\quad for \quad x ≤ 1 \\ 2x - 2, \quad when\quad x ≥ 1 \end(cases) \end(equation*) \begin(equation*)f"(x)=0,\quad when\quad x= \begin(cases) 2,\quad when \quad x ≤ 1 \\ 1,\quad for \quad x ≥ 1 \end(cases) \end(equation*) So, we have two stationary points and let's not forget that our function consists of two functions for different x.
Let's find the largest and smallest values ​​of the function, for this we calculate the values ​​of the function at stationary points and at the ends of the segment:
Answer: The function reaches its minimum value at the stationary point x= 1, y at least. = 3. The function reaches its maximum value at the end of the segment at the point x= 4, y max. = 12.

Example

Find the maximum value of the function y= $\frac(3x)(x^2 + 3)$ on the ray: , b) , c) [-4;7].
b) Find the largest and smallest value of the function y= x 2 - 6x + 8 + |x - 2| on the interval [-1;5].
c) Find the largest and smallest value of the function y= $-2x-\frac(1)(2x)$ on the ray (0;+∞).

The process of finding the smallest and largest values ​​of a function on a segment is reminiscent of a fascinating flight around an object (a graph of a function) on a helicopter with firing from a long-range cannon at certain points and choosing from these points very special points for control shots. Points are selected in a certain way and according to certain rules. By what rules? We will talk about this further.

If the function y = f(x) continuous on the segment [ a, b] , then it reaches on this segment least And highest values . This can either happen in extremum points or at the ends of the segment. Therefore, to find least And the largest values ​​of the function , continuous on the segment [ a, b] , you need to calculate its values ​​in all critical points and at the ends of the segment, and then choose the smallest and largest of them.

Let, for example, it is required to determine the maximum value of the function f(x) on the segment [ a, b] . To do this, find all its critical points lying on [ a, b] .

critical point is called the point at which function defined, and her derivative is either zero or does not exist. Then you should calculate the values ​​of the function at critical points. And, finally, one should compare the values ​​of the function at critical points and at the ends of the segment ( f(a) And f(b) ). The largest of these numbers will be the largest value of the function on the segment [a, b] .

The problem of finding the smallest values ​​of the function .

We are looking for the smallest and largest values ​​​​of the function together

Example 1. Find the smallest and largest values ​​of a function on the segment [-1, 2] .

Solution. We find the derivative of this function. Equate the derivative to zero () and get two critical points: and . To find the smallest and largest values ​​of a function on a given segment, it is enough to calculate its values ​​at the ends of the segment and at the point , since the point does not belong to the segment [-1, 2] . These function values ​​are the following: , , . It follows that smallest function value(marked in red in the graph below), equal to -7, is reached at the right end of the segment - at the point , and greatest(also red on the graph), is equal to 9, - at the critical point .

If the function is continuous in a certain interval and this interval is not a segment (but is, for example, an interval; the difference between an interval and a segment: the boundary points of the interval are not included in the interval, but the boundary points of the segment are included in the segment), then among the values ​​of the function there may not be be the smallest and largest. So, for example, the function depicted in the figure below is continuous on ]-∞, +∞[ and does not have the largest value.

However, for any interval (closed, open, or infinite), the following property of continuous functions holds.

Example 4. Find the smallest and largest values ​​of a function on the segment [-1, 3] .

Solution. We find the derivative of this function as the derivative of the quotient:

.

We equate the derivative to zero, which gives us one critical point: . It belongs to the interval [-1, 3] . To find the smallest and largest values ​​of a function on a given segment, we find its values ​​at the ends of the segment and at the found critical point:

Let's compare these values. Conclusion: equal to -5/13, at the point and the greatest value equal to 1 at the point .

We continue to search for the smallest and largest values ​​​​of the function together

There are teachers who, on the topic of finding the smallest and largest values ​​of a function, do not give students examples more complicated than those just considered, that is, those in which the function is a polynomial or a fraction, the numerator and denominator of which are polynomials. But we will not limit ourselves to such examples, since among teachers there are lovers of making students think in full (table of derivatives). Therefore, the logarithm and the trigonometric function will be used.

Example 6. Find the smallest and largest values ​​of a function on the segment .

Solution. We find the derivative of this function as derivative of the product :

We equate the derivative to zero, which gives one critical point: . It belongs to the segment. To find the smallest and largest values ​​of a function on a given segment, we find its values ​​at the ends of the segment and at the found critical point:

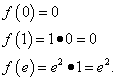
The result of all actions: the function reaches its minimum value, equal to 0, at a point and at a point and the greatest value equal to e² , at the point .

Example 7. Find the smallest and largest values ​​of a function on the segment .

Solution. We find the derivative of this function:

Equate the derivative to zero:

The only critical point belongs to the segment . To find the smallest and largest values ​​of a function on a given segment, we find its values ​​at the ends of the segment and at the found critical point:

Output: the function reaches its minimum value, equal to , at the point and the greatest value, equal to , at the point .

In applied extremal problems, finding the smallest (largest) function values, as a rule, is reduced to finding the minimum (maximum). But it is not the minima or maxima themselves that are of greater practical interest, but the values ​​of the argument at which they are achieved. When solving applied problems, an additional difficulty arises - the compilation of functions that describe the phenomenon or process under consideration.

Example 8 A tank with a capacity of 4, having the shape of a parallelepiped with a square base and open at the top, must be tinned. What should be the dimensions of the tank in order to cover it with the least amount of material?

Solution. Let be x- base side h- tank height, S- its surface area without cover, V- its volume. The surface area of ​​the tank is expressed by the formula , i.e. is a function of two variables. To express S as a function of one variable, we use the fact that , whence . Substituting the found expression h into the formula for S:

Let us examine this function for an extremum. It is defined and differentiable everywhere in ]0, +∞[ , and

.

We equate the derivative to zero () and find the critical point. In addition, at , the derivative does not exist, but this value is not included in the domain of definition and therefore cannot be an extremum point. So, - the only critical point. Let's check it for the presence of an extremum using the second sufficient sign. Let's find the second derivative. When the second derivative is greater than zero (). This means that when the function reaches a minimum . Because this minimum - the only extremum of this function, it is its smallest value. So, the side of the base of the tank should be equal to 2 m, and its height.

Example 9 From paragraph A, located on the railway line, to the point FROM, at a distance from it l, goods must be transported. The cost of transporting a weight unit per unit distance by rail is equal to , and by highway it is equal to . To what point M railroad line should be held highway to transport cargo from BUT in FROM was the most economical AB railroad is assumed to be straight)?