Zakon raspodjele slučajne varijable x dan je tablicom. Diskretna slučajna varijabla i njezine numeričke karakteristike. Formula za zbrajanje vjerojatnosti
Definicija 1
Slučajna varijabla $X$ naziva se diskretnom (diskontinuiranom) ako je skup njezinih vrijednosti beskonačan ili konačan, ali prebrojiv.
Drugim riječima, veličina se naziva diskretnom ako se njezine vrijednosti mogu numerirati.
Slučajna varijabla može se opisati pomoću zakona distribucije.
Zakon distribucije diskretne slučajne varijable $X$ može se zadati u obliku tablice u kojoj su u prvom retku sve moguće vrijednosti slučajne varijable u rastućem redoslijedu, a u drugom retku su odgovarajuće vjerojatnosti tih vrijednosti:
Slika 1.
gdje je $r1+ r2+ ... + rn = 1$.
Ova tablica je blizu distribucije diskretne slučajne varijable.
Ako je skup mogućih vrijednosti slučajne varijable beskonačan, tada niz $r1+ r2+ ... + rn+ ...$ konvergira i njegova suma će biti jednaka $1$.
Zakon distribucije diskretne slučajne varijable $X$ može se prikazati grafički, za što se u koordinatnom sustavu konstruira izlomljena linija (pravokutnik), koja sekvencijalno povezuje točke s koordinatama $(xi;pi), i=1,2, ... n$. Linija koju smo dobili zove se distribucijski poligon.

Slika 2.
Zakon distribucije diskretne slučajne varijable $X$ može se prikazati i analitički (pomoću formule):
$P(X=xi)= \varphi (xi),i =1,2,3 ... n$.
Operacije na diskretnim vjerojatnostima
Pri rješavanju mnogih problema u teoriji vjerojatnosti potrebno je izvesti operacije množenja diskretne slučajne varijable s konstantom, zbrajanja dviju slučajnih varijabli, njihovog množenja, zamjene na potenciju. U tim slučajevima potrebno je pridržavati se sljedećih pravila za slučajne diskretne veličine:
Definicija 3
Množenje diskretna slučajna varijabla $X$ konstantom $K$ naziva se diskretnom slučajna vrijednost$Y=KX,$ što je određeno jednakostima: $y_i=Kx_i,\ \ p\left(y_i\right)=p\left(x_i\right)=p_i,\ \ i=\overline(1,\ n) $
Definicija 4
Pozivaju se dvije slučajne varijable $x$ i $y$ nezavisna, ako zakon raspodjele jedne od njih ne ovisi o tome koje je moguće vrijednosti stekla druga količina.
Definicija 5
Iznos dvije neovisne diskretne slučajne varijable $X$ i $Y$ nazivaju se slučajna varijabla $Z=X+Y,$ određena je jednakostima: $z_(ij)=x_i+y_j$, $P\left(z_(ij )\desno)= P\lijevo(x_i\desno)P\lijevo(y_j\desno)=p_ip"_j$, $i=\overline(1,n)$, $j=\overline(1,m)$ , $P\lijevo (x_i\desno)=p_i$, $P\lijevo(y_j\desno)=p"_j$.
Definicija 6
Množenje dvije neovisne diskretne slučajne varijable $X$ i $Y$ nazivaju se slučajna varijabla $Z=XY,$ određena je jednakostima: $z_(ij)=x_iy_j$, $P\lijevo(z_(ij)\desno) =P\lijevo( x_i\desno)P\lijevo(y_j\desno)=p_ip"_j$, $i=\overline(1,n)$, $j=\overline(1,m)$, $P\ lijevo(x_i\desno )=p_i$, $P\lijevo(y_j\desno)=p"_j$.
Uzmimo u obzir da neki umnošci $x_(i\ \ \ \ \ )y_j$ mogu biti međusobno jednaki. U tom je slučaju vjerojatnost zbrajanja umnoška jednaka zbroju odgovarajućih vjerojatnosti.
Na primjer, ako je $x_2\ \ y_3=x_5\ \ y_7,\ $tada će vjerojatnost $x_2y_3$ (ili istog $x_5y_7$) biti jednaka $p_2\cdot p"_3+p_5\cdot p"_7 .$
Gore navedeno vrijedi i za iznos. Ako je $x_1+\ y_2=x_4+\ \ y_6,$ tada će vjerojatnost $x_1+\ y_2$ (ili istog $x_4+\ y_6$) biti jednaka $p_1\cdot p"_2+p_4\cdot p"_6. $
Slučajne varijable $X$ i $Y$ određene su zakonima distribucije:
Slika 3.
Gdje je $p_1+p_2+p_3=1,\ \ \ p"_1+p"_2=1.$ Tada će zakon raspodjele zbroja $X+Y$ imati oblik
Slika 4.
I zakon distribucije proizvoda $XY$ će imati oblik
Slika 5.
Funkcija distribucije
Potpuni opis slučajne varijable također daje funkcija distribucije.
Geometrijski, funkcija distribucije se objašnjava kao vjerojatnost da slučajna varijabla $X$ poprimi vrijednost koja je na brojevnom pravcu predstavljena točkom koja leži lijevo od točke $x$.
ZAKON DISTRIBUCIJE I KARAKTERISTIKE
SLUČAJNE VARIJABLE
Slučajne varijable, njihova klasifikacija i metode opisa.
Slučajna veličina je veličina koja kao rezultat pokusa može poprimiti jednu ili drugu vrijednost, ali nije unaprijed poznato koju. Za slučajnu varijablu, dakle, možete specificirati samo vrijednosti, od kojih će jednu sigurno uzeti kao rezultat eksperimenta. U nastavku ćemo ove vrijednosti zvati moguće vrijednosti slučajne varijable. Budući da slučajna varijabla kvantitativno karakterizira slučajni rezultat eksperimenta, može se smatrati kao kvantitativna karakteristika slučajni događaj.
Slučajne varijable obično se označavaju velikim slovima latinične abecede, na primjer, X..Y..Z, a njihove moguće vrijednosti odgovarajućim malim slovima.
Postoje tri vrste slučajnih varijabli:
Diskretna; Stalan; Mješoviti.
Diskretna je slučajna varijabla čiji broj mogućih vrijednosti čini prebrojiv skup. Zauzvrat, skup čiji se elementi mogu numerirati nazivamo prebrojivim. Riječ "diskretan" dolazi od latinske riječi discretus, što znači "diskontinuiran, koji se sastoji od pojedini dijelovi» .
Primjer 1. Diskretna slučajna varijabla je broj neispravnih dijelova X u seriji od n proizvoda. Doista, moguće vrijednosti ove slučajne varijable su niz cijelih brojeva od 0 do n.
Primjer 2. Diskretna slučajna varijabla je broj hitaca prije prvog pogotka u metu. Ovdje, kao u primjeru 1, moguće vrijednosti mogu biti numerirane, iako je u graničnom slučaju moguća vrijednost beskonačno velik broj.
Stalan je slučajna varijabla čije moguće vrijednosti kontinuirano ispunjavaju određeni interval numeričke osi, koji se ponekad naziva i interval postojanja ove slučajne varijable. Dakle, na bilo kojem konačnom intervalu postojanja, broj mogućih vrijednosti kontinuirane slučajne varijable je beskonačno velik.
Primjer 3. Kontinuirana slučajna varijabla je mjesečna potrošnja električne energije poduzeća.
Primjer 4. Kontinuirana slučajna varijabla je pogreška u mjerenju visine pomoću visinomjera. Neka je iz principa rada visinomjera poznato da se pogreška nalazi u rasponu od 0 do 2 m. Dakle, interval postojanja ove slučajne varijable je interval od 0 do 2 m.
Zakon raspodjele slučajnih varijabli.
Slučajna varijabla smatra se potpuno određenom ako su njene moguće vrijednosti naznačene na numeričkoj osi i ako je uspostavljen zakon distribucije.
Zakon raspodjele slučajne varijable je relacija koja uspostavlja vezu između mogućih vrijednosti slučajne varijable i odgovarajućih vjerojatnosti.
Kaže se da je slučajna varijabla raspodijeljena prema danom zakonu ili podložna danom zakonu distribucije. Brojne vjerojatnosti, funkcija distribucije, gustoća vjerojatnosti i karakteristična funkcija koriste se kao zakoni distribucije.
Zakon raspodjele daje potpuni vjerojatni opis slučajne varijable. Prema zakonu raspodjele, prije eksperimenta se može prosuditi koje će se moguće vrijednosti slučajne varijable pojavljivati češće, a koje rjeđe.
Za diskretnu slučajnu varijablu zakon raspodjele može se zadati u obliku tablice, analitički (u obliku formule) i grafički.
Najjednostavniji oblik definiranje zakona distribucije diskretne slučajne varijable je tablica (matrica) u kojoj su sve moguće vrijednosti slučajne varijable i njihove odgovarajuće vjerojatnosti navedene uzlaznim redoslijedom, tj.
![]()
Takva se tablica naziva serija distribucije diskretne slučajne varijable. 1
Događaji X 1, X 2,..., X n, koji se sastoje u činjenici da će kao rezultat testa slučajna varijabla X poprimiti vrijednosti x 1, x 2,... x n, redom, su nekonzistentne i jedine moguće (budući da su u tablici navedene sve moguće vrijednosti slučajne varijable), tj. čine kompletnu grupu. Stoga je zbroj njihovih vjerojatnosti jednak 1. Dakle, za bilo koju diskretnu slučajnu varijablu
![]()
(Ova jedinica je nekako raspoređena među vrijednostima slučajne varijable, otuda i izraz "distribucija").
Niz distribucije može se grafički prikazati ako se vrijednosti slučajne varijable nanesu na apscisnu os, a njihove odgovarajuće vjerojatnosti na ordinatnu os. Spoj dobivenih točaka čini isprekidanu liniju koja se naziva poligon ili poligon distribucije vjerojatnosti (slika 1).

Primjer Lutrija uključuje: automobil u vrijednosti od 5.000 den. kom., 4 televizora po 250 den. jedinica, 5 video rekordera u vrijednosti od 200 den. jedinice Za 7 dana prodano je ukupno 1000 ulaznica. jedinice Napravite zakon o raspodjeli neto dobitka koji je dobio sudionik lutrije koji je kupio jedan listić.
Riješenje. Moguće vrijednosti slučajne varijable X - neto dobitak po listiću - jednake su 0-7 = -7 novca. jedinice (ako listić nije dobio), 200-7 = 193, 250-7 = 243, 5000-7 = 4993 den. jedinice (ako listić sadrži dobitke od videorekordera, televizora ili automobila). Uzimajući u obzir da je od 1000 listića broj nedobitnih 990, a naznačeni dobici su 5, 4 i 1 redom, te korištenjem klasične definicije vjerojatnosti dobivamo.
Poglavlje 1. Diskretna slučajna varijabla
§ 1. Pojmovi slučajne varijable.
Zakon distribucije diskretne slučajne varijable.
Definicija : Slučajna je veličina koja, kao rezultat testiranja, uzima samo jednu vrijednost iz mogućeg skupa svojih vrijednosti, unaprijed nepoznatih i ovisno o slučajnim razlozima.
Postoje dvije vrste slučajnih varijabli: diskretne i kontinuirane.
Definicija : Poziva se slučajna varijabla X diskretna (diskontinuiran) ako je skup njegovih vrijednosti konačan ili beskonačan, ali prebrojiv.
Drugim riječima, moguće vrijednosti diskretne slučajne varijable mogu se prenumerirati.
Slučajna varijabla može se opisati korištenjem zakona distribucije.
Definicija : Zakon distribucije diskretne slučajne varijable nazvati korespondenciju između mogućih vrijednosti slučajne varijable i njihove vjerojatnosti.
Zakon raspodjele diskretne slučajne varijable X može se specificirati u obliku tablice, u čijem su prvom retku sve moguće vrijednosti slučajne varijable naznačene uzlaznim redoslijedom, au drugom redu odgovarajuće vjerojatnosti tih vrijednosti, tj.
gdje je r1+ r2+…+ rn=1
Takva se tablica naziva serija distribucije diskretne slučajne varijable.
Ako je skup mogućih vrijednosti slučajne varijable beskonačan, tada niz p1+ p2+…+ pn+… konvergira i njegov zbroj je jednak 1.
Zakon raspodjele diskretne slučajne varijable X može se prikazati grafički, za što pravokutni sustav koordinatama, polilinija se konstruira povezujući uzastopne točke s koordinatama (xi; pi), i=1,2,…n. Rezultirajući pravac naziva se distribucijski poligon (Sl. 1).
Organska kemija" href="/text/category/organicheskaya_hiimya/" rel="bookmark">organska kemija su 0,7 odnosno 0,8. Napravite zakon raspodjele za slučajnu varijablu X - broj ispita koje će student položiti.
Riješenje. Razmatrana slučajna varijabla X kao rezultat ispita može poprimiti jednu od sljedećih vrijednosti: x1=0, x2=1, x3=2.
Nađimo vjerojatnost ovih vrijednosti Označimo događaje:
https://pandia.ru/text/78/455/images/image004_81.jpg" width="259" height="66 src=">
 |
Dakle, zakon raspodjele slučajne varijable X dan je tablicom:
Kontrola: 0,6+0,38+0,56=1.
§ 2. Funkcija distribucije
Potpuni opis slučajne varijable također daje funkcija distribucije.
Definicija: Funkcija distribucije diskretne slučajne varijable X naziva se funkcija F(x), koja za svaku vrijednost x određuje vjerojatnost da će slučajna varijabla X poprimiti vrijednost manju od x:
F(x)=P(X<х)
Geometrijski, funkcija distribucije tumači se kao vjerojatnost da će slučajna varijabla X poprimiti vrijednost koja je na brojevnom pravcu predstavljena točkom koja leži lijevo od točke x.
1)0≤ F(x) ≤1;
2) F(x) je neopadajuća funkcija na (-∞;+∞);
3) F(x) - kontinuirano lijevo u točkama x= xi (i=1,2,...n) i kontinuirano u svim ostalim točkama;
4) F(-∞)=P (X<-∞)=0 как вероятность невозможного события Х<-∞,
F(+∞)=P(X<+∞)=1 как вероятность достоверного события Х<-∞.
Ako je zakon raspodjele diskretne slučajne varijable X dan u obliku tablice:
tada je funkcija distribucije F(x) određena formulom:
https://pandia.ru/text/78/455/images/image007_76.gif" height="110">
0 za x≤ x1,
r1 na x1< х≤ x2,
F(x)= r1 + r2 u x2< х≤ х3
1 za x>xn.
Njegov graf je prikazan na sl. 2:

§ 3. Numeričke karakteristike diskretne slučajne varijable.
Jedna od važnih numeričkih karakteristika je matematičko očekivanje.
Definicija: Matematičko očekivanje M(X) diskretna slučajna varijabla X je zbroj umnožaka svih njezinih vrijednosti i njihovih odgovarajućih vjerojatnosti:
M(X) = ∑ xiri= x1r1 + x2r2+…+ xnrn
Matematičko očekivanje služi kao karakteristika prosječne vrijednosti slučajne varijable.
Svojstva matematičkog očekivanja:
1)M(C)=C, gdje je C konstantna vrijednost;
2)M(C X)=C M(X),
3)M(X±Y)=M(X)±M(Y);
4)M(X Y)=M(X) M(Y), gdje su X, Y nezavisne slučajne varijable;
5)M(X±C)=M(X)±C, gdje je C konstantna vrijednost;
Za karakterizaciju stupnja disperzije mogućih vrijednosti diskretne slučajne varijable oko njezine srednje vrijednosti koristi se disperzija.
Definicija: Varijanca D ( x ) slučajna varijabla X je matematičko očekivanje kvadrata odstupanja slučajne varijable od njenog matematičkog očekivanja:
Disperzijska svojstva:
1)D(C)=0, gdje je C konstantna vrijednost;
2)D(X)>0, gdje je X slučajna varijabla;
3)D(C X)=C2 D(X), gdje je C konstantna vrijednost;
4)D(X+Y)=D(X)+D(Y), gdje su X, Y nezavisne slučajne varijable;
Za izračun varijance često je zgodno koristiti formulu:
D(X)=M(X2)-(M(X))2,
gdje je M(X)=∑ xi2ri= x12r1 + x22r2+…+ xn2rn
Varijanca D(X) ima dimenziju kvadrata slučajne varijable, što nije uvijek zgodno. Stoga se vrijednost √D(X) također koristi kao pokazatelj disperzije mogućih vrijednosti slučajne varijable.
Definicija: Standardna devijacija σ(X) slučajna varijabla X naziva se kvadratni korijen varijance:
![]()
Zadatak br. 2. Diskretna slučajna varijabla X određena je zakonom distribucije:
Nađite P2, funkciju distribucije F(x) i nacrtajte njen graf, kao i M(X), D(X), σ(X).
Riješenje: Budući da je zbroj vjerojatnosti mogućih vrijednosti slučajne varijable X jednak 1, tada
R2=1- (0,1+0,3+0,2+0,3)=0,1
Nađimo funkciju distribucije F(x)=P(X Geometrijski, ova se jednakost može protumačiti na sljedeći način: F(x) je vjerojatnost da će slučajna varijabla poprimiti vrijednost koja je na brojčanoj osi predstavljena točkom koja leži lijevo od točke x. Ako je x≤-1, tada je F(x)=0, jer ne postoji niti jedna vrijednost ove slučajne varijable na (-∞;x); Ako je -1<х≤0, то F(х)=Р(Х=-1)=0,1, т. к. в промежуток (-∞;х) попадает только одно значение x1=-1; Ako je 0<х≤1, то F(х)=Р(Х=-1)+ Р(Х=0)=0,1+0,1=0,2, т. к. в промежуток (-∞;x) postoje dvije vrijednosti x1=-1 i x2=0; Ako 1<х≤2, то F(х)=Р(Х=-1) + Р(Х=0)+ Р(Х=1)= 0,1+0,1+0,3=0,5, т. к. в промежуток (-∞;х) попадают три значения x1=-1, x2=0 и x3=1; Ako 2<х≤3, то F(х)=Р(Х=-1) + Р(Х=0)+ Р(Х=1)+ Р(Х=2)= 0,1+0,1+0,3+0,2=0,7, т. к. в промежуток (-∞;х) попадают четыре значения x1=-1, x2=0,x3=1 и х4=2; Ako je x>3, tada je F(x)=P(X=-1) + P(X=0)+ P(X=1)+ P(X=2)+P(X=3)= 0,1 +0,1 +0,3+0,2+0,3=1, jer četiri vrijednosti x1=-1, x2=0, x3=1, x4=2 spadaju u interval (-∞;x) i x5=3. https://pandia.ru/text/78/455/images/image006_89.gif" width="14 height=2" height="2"> 0 pri x≤-1, 0,1 na -1<х≤0, 0,2 na 0<х≤1, F(x)= 0,5 na 1<х≤2, 0,7 na 2<х≤3, 1 na x>3 Predstavimo funkciju F(x) grafički (slika 3): https://pandia.ru/text/78/455/images/image014_24.jpg" width="158 height=29" height="29">≈1,2845. §
4. Binomni zakon raspodjele diskretna slučajna varijabla, Poissonov zakon. Definicija: Binomni
naziva se zakon distribucije diskretne slučajne varijable X - broj pojavljivanja događaja A u n neovisnih ponovljenih pokušaja, u svakom od kojih se događaj A može dogoditi s vjerojatnošću p ili ne dogoditi s vjerojatnošću q = 1-p. Tada se P(X=m) - vjerojatnost pojavljivanja događaja A točno m puta u n pokušaja izračunava pomoću Bernoullijeve formule: R(H=m)=Smnpmqn-m Matematičko očekivanje, disperzija i standardna devijacija slučajne varijable X raspoređene prema binarnom zakonu nalaze se pomoću formula: https://pandia.ru/text/78/455/images/image016_31.gif" width="26"> Vjerojatnost događaja A - "ispadanje petice" u svakom pokušaju je ista i jednaka 1/6 , tj. P(A)=p=1/6, tada P(A)=1-p=q=5/6, gdje je - "nedobivanje A." Slučajna varijabla X može poprimiti sljedeće vrijednosti: 0;1;2;3. Pronalazimo vjerojatnost svake od mogućih vrijednosti X pomoću Bernoullijeve formule: R(H=0)=R3(0)=S03r0q3=1 (1/6)0 (5/6)3=125/216; R(H=1)=R3(1)=S13r1q2=3 (1/6)1 (5/6)2=75/216; R(H=2)=R3(2)=S23r2q =3 (1/6)2 (5/6)1=15/216; R(H=3)=R3(3)=S33r3q0=1 (1/6)3 (5/6)0=1/216. Da. zakon distribucije slučajne varijable X ima oblik: Kontrola: 125/216+75/216+15/216+1/216=1. Nađimo numeričke karakteristike slučajne varijable X: M(X)=np=3 (1/6)=1/2, D(X)=npq=3 (1/6) (5/6)=5/12, Zadatak br. 4. Automatski stroj štanca dijelove. Vjerojatnost da će proizvedeni dio biti neispravan je 0,002. Odredite vjerojatnost da će među 1000 odabranih dijelova biti: a) 5 neispravnih; b) najmanje jedan je neispravan. Riješenje:
Broj n=1000 je velik, vjerojatnost proizvodnje neispravnog dijela p=0,002 je mala, a događaji koji se razmatraju (pokazuje se da je dio neispravan) su neovisni, stoga vrijedi Poissonova formula: Rn(m)= e-
λ
λm Nađimo λ=np=1000 0,002=2. a) Odredite vjerojatnost da će biti 5 neispravnih dijelova (m=5): R1000(5)= e-2
25
= 32 0,13534
= 0,0361 b) Odredite vjerojatnost da će biti barem jedan neispravan dio. Događaj A - "barem jedan od odabranih dijelova je neispravan" suprotan je događaju - "svi odabrani dijelovi nisu neispravni." Prema tome, P(A) = 1-P(). Stoga je željena vjerojatnost jednaka: P(A)=1-P1000(0)=1- e-2
20
= 1- e-2=1-0,13534≈0,865. Zadaci za samostalan rad.
1.1
1.2.
Raspršena slučajna varijabla X određena je zakonom distribucije: Nađite p4, funkciju distribucije F(X) i nacrtajte njen graf, kao i M(X), D(X), σ(X). 1.3.
U kutiji je 9 markera, od kojih 2 više ne pišu. Nasumično uzmite 3 markera. Slučajna varijabla X je broj markera za pisanje među uzetima. Nacrtati zakon raspodjele slučajne varijable. 1.4.
Na polici knjižnice nalazi se 6 udžbenika nasumično poredanih, od kojih su 4 uvezana. Knjižničar nasumce uzima 4 udžbenika. Slučajna varijabla X je broj ukoričenih udžbenika među uzetima. Nacrtati zakon raspodjele slučajne varijable. 1.5.
Na listiću su dva zadatka. Vjerojatnost prava odluka prvi problem je 0,9, drugi je 0,7. Slučajna varijabla X je broj točno riješenih zadataka na listiću. Nacrtajte zakon distribucije, izračunajte matematičko očekivanje i varijancu ove slučajne varijable, a također pronađite funkciju distribucije F(x) i izgradite njezin grafikon. 1.6.
Tri strijelca gađaju metu. Vjerojatnost pogotka mete jednim hicem je 0,5 za prvog strijelca, 0,8 za drugog i 0,7 za trećeg. Slučajna varijabla X je broj pogodaka u metu ako strijelci pucaju jedan po jedan. Pronađite zakon raspodjele, M(X),D(X). 1.7.
Košarkaš ubacuje loptu u koš s vjerojatnošću da će pogoditi svaki šut od 0,8. Za svaki pogodak dobiva 10 bodova, a ako promaši ne dobiva bodove. Nacrtajte zakon raspodjele za slučajnu varijablu X - broj poena koje je košarkaš primio u 3 udarca. Nađite M(X),D(X), kao i vjerojatnost da dobije više od 10 bodova. 1.8.
Na karticama su ispisana slova, ukupno 5 samoglasnika i 3 suglasnika. Nasumično se biraju 3 karte i svaki put se uzeta karta vraća natrag. Slučajna varijabla X je broj samoglasnika među uzetima. Nacrtajte zakon raspodjele i pronađite M(X),D(X),σ(X). 1.9.
U prosjeku 60% ugovora Osiguravajuće društvo isplaćuje iznose osiguranja u svezi s nastupom osiguranog slučaja. Napravite zakon raspodjele za slučajnu varijablu X - broj ugovora za koje je isplaćen iznos osiguranja među četiri slučajno odabrana ugovora. Odredite brojčane karakteristike te veličine. 1.10.
Radio postaja šalje pozivne znakove (ne više od četiri) u određenim intervalima dok se ne uspostavi dvosmjerna komunikacija. Vjerojatnost primanja odgovora na pozivni znak je 0,3. Slučajna varijabla X je broj poslanih pozivnih znakova. Nacrtajte zakon raspodjele i pronađite F(x). 1.11.
Ima 3 ključa od kojih samo jedan odgovara bravi. Napravite zakon raspodjele slučajne varijable X-broj pokušaja otvaranja brave, ako isprobani ključ ne sudjeluje u sljedećim pokušajima. Pronađite M(X),D(X). 1.12.
Provedena su uzastopna neovisna testiranja pouzdanosti tri uređaja. Svaki sljedeći uređaj testira se samo ako se prethodni pokazao pouzdanim. Vjerojatnost prolaska testa za svaki uređaj je 0,9. Nacrtajte zakon raspodjele za slučajnu varijablu X-broj testiranih uređaja. 1.13
.Diskretna slučajna varijabla X ima tri moguće vrijednosti: x1=1, x2, x3 i x1<х2<х3. Вероятность того, что Х примет значения х1 и х2, соответственно равны 0,3 и 0,2. Известно, что М(Х)=2,2, D(X)=0,76. Составить закон распределения случайной величины. 1.14.
Blok elektroničkog uređaja sadrži 100 identičnih elemenata. Vjerojatnost kvara svakog elementa tijekom vremena T je 0,002. Elementi rade neovisno. Odredite vjerojatnost da tijekom vremena T neće otkazati više od dva elementa. 1.15.
Udžbenik je objavljen u nakladi od 50.000 primjeraka. Vjerojatnost da je udžbenik krivo uvezan je 0,0002. Odredite vjerojatnost da cirkulacija sadrži: a) četiri neispravne knjige, b) manje od dvije neispravne knjige. 1
.16.
Broj poziva koji pristignu na PBX svake minute raspoređuje se prema Poissonovom zakonu s parametrom λ=1,5. Nađite vjerojatnost da će za minutu stići sljedeće: a) dva poziva; b) najmanje jedan poziv. 1.17.
Nađite M(Z),D(Z) ako je Z=3X+Y. 1.18.
Dati su zakoni raspodjele dviju neovisnih slučajnih varijabli: Nađite M(Z),D(Z) ako je Z=X+2Y. odgovori:
https://pandia.ru/text/78/455/images/image007_76.gif" height="110"> 1.1.
p3=0,4; 0 pri x≤-2, 0,3 na -2<х≤0, F(x)= 0,5 na 0<х≤2, 0,9 u 2<х≤5, 1 na x>5 0,3 na -1<х≤0, 0,4 na 0<х≤1, F(x)= 0,6 na 1<х≤2, 0,7 na 2<х≤3, 1 na x>3 M(X)=1; D(X)=2,6; σ(X) ≈1,612. https://pandia.ru/text/78/455/images/image025_24.gif" width="2 height=98" height="98"> 0 na x≤0, 0,03 na 0<х≤1, F(x)= 0,37 na 1<х≤2, 1 za x>2 M(X)=2; D(X)=0,62 M(X)=2,4; D(X)=0,48, P(X>10)=0,896 1.
8
.
M(X)=15/8; D(X)=45/64; σ(X) ≈ M(X)=2,4; D(X)=0,96 https://pandia.ru/text/78/455/images/image008_71.gif" width="14"> 1.11.
M(X)=2; D(X)=2/3 1.14.
1,22 e-0,2≈0,999 1.15.
a) 0,0189; b) 0,00049 1.16.
a) 0,0702; b) 0,77687 1.17.
3,8; 14,2 1.18.
11,2; 4. 2. Poglavlje. Kontinuirana slučajna varijabla
Definicija: Stalan
Veličinom se nazivaju sve moguće vrijednosti od kojih u potpunosti ispunjavaju konačni ili beskonačni raspon brojevnog pravca. Očito je da je broj mogućih vrijednosti kontinuirane slučajne varijable beskonačan. Kontinuirana slučajna varijabla može se odrediti pomoću funkcije distribucije. Definicija: F distribucijska funkcija
kontinuirana slučajna varijabla X naziva se funkcija F(x), koja za svaku vrijednost određuje xhttps://pandia.ru/text/78/455/images/image028_11.jpg" width="14" height="13"> R Funkcija distribucije se ponekad naziva i kumulativna funkcija distribucije. Svojstva funkcije distribucije:
1)1≤ F(x) ≤1 2) Za kontinuiranu slučajnu varijablu, funkcija distribucije je kontinuirana u bilo kojoj točki i diferencijabilna posvuda, osim, možda, u pojedinačnim točkama. 3) Vjerojatnost da slučajna varijabla X padne u jedan od intervala (a;b), [a;b], [a;b], jednaka je razlici između vrijednosti funkcije F(x) u točkama a i b, tj. R(a)<Х 4) Vjerojatnost da će kontinuirana slučajna varijabla X poprimiti jednu zasebnu vrijednost je 0. 5) F(-∞)=0, F(+∞)=1 Određivanje kontinuirane slučajne varijable pomoću funkcije distribucije nije jedini način. Uvedimo pojam gustoće distribucije vjerojatnosti (gustoće distribucije). Definicija
:
Gustoća distribucije vjerojatnosti
f
(
x
)
kontinuirane slučajne varijable X je derivacija njene distribucijske funkcije, tj.: Funkcija gustoće vjerojatnosti ponekad se naziva funkcija diferencijalne distribucije ili zakon diferencijalne distribucije. Graf distribucije gustoće vjerojatnosti f(x) naziva se krivulja distribucije vjerojatnosti
.
Svojstva distribucije gustoće vjerojatnosti:
1) f(x) ≥0, na xhttps://pandia.ru/text/78/455/images/image029_10.jpg" width="285" height="141">DIV_ADBLOCK92"> https://pandia.ru/text/78/455/images/image032_23.gif" height="38 src="> +∞ 2 6 +∞ 6 6 ∫ f(x)dx=∫ 0dx+ ∫ c(x-2)dx +∫ 0dx= c∫ (x-2)dx=c(x2/2-2x) =c(36/2-12-(4/ 2-4))=8s; b) Poznato je da je F(x)= ∫ f(x)dx Stoga, x ako je x≤2, tada je F(x)= ∫ 0dx=0; https://pandia.ru/text/78/455/images/image032_23.gif" height="38 src="> 2 6 x 6 6 ako je x>6, tada je F(x)= ∫ 0dx+∫ 1/8(x-2)dx+∫ 0dx=1/8∫(x-2)dx=1/8(x2/2-2x) = 1/8(36/2-12-(4/2+4))=1/8 8=1. Tako, 0 pri x≤2, F(x)= (x-2)2/16 na 2<х≤6, 1 za x>6. Graf funkcije F(x) prikazan je na slici 3 https://pandia.ru/text/78/455/images/image034_23.gif" width="14" height="62 src="> 0 na x≤0, F(x)= (3 arctan x)/π na 0<х≤√3, 1 za x>√3. Pronađite funkciju diferencijalne distribucije f(x) Riješenje:
Budući da je f(x)= F’(x), tada DIV_ADBLOCK93"> · Matematičko očekivanje M (X)
kontinuirana slučajna varijabla X određena je jednakošću: M(X)= ∫ x f(x)dx, uz uvjet da taj integral apsolutno konvergira. · Disperzija
D
(
x
)
kontinuirana slučajna varijabla X određena je jednakošću: D(X)= ∫ (x-M(x)2) f(x)dx, ili D(X)= ∫ x2 f(x)dx - (M(x))2 · Standardna devijacija σ(X)
kontinuirana slučajna varijabla određena je jednakošću: Sva svojstva matematičkog očekivanja i disperzije, koja su ranije razmatrana za disperzirane slučajne varijable, vrijede i za one kontinuirane. Zadatak br. 3. Slučajna varijabla X određena je diferencijalnom funkcijom f(x): https://pandia.ru/text/78/455/images/image036_19.gif" height="38"> -∞ 2 X3/9 + x2/6 = 8/9-0+9/6-4/6=31/18, https://pandia.ru/text/78/455/images/image032_23.gif" height="38"> +∞ D(X)= ∫ x2 f(x)dx-(M(x))2=∫ x2 x/3 dx+∫1/3x2 dx=(31/18)2=x4/12 + x3/9 - - (31/18)2=16/12-0+27/9-8/9-(31/18)2=31/9- (31/18)2==31/9(1-31/36)=155/324, https://pandia.ru/text/78/455/images/image032_23.gif" height="38"> P(1<х<5)= ∫ f(x)dx=∫ х/3 dx+∫ 1/3 dx+∫ 0 dx= х2/6 +1/3х = 4/6-1/6+1-2/3=5/6. Problemi za samostalno rješavanje.
2.1.
Kontinuirana slučajna varijabla X određena je funkcijom distribucije: 0 pri x≤0, F(x)= https://pandia.ru/text/78/455/images/image038_17.gif" width="14" height="86"> 0 za x≤ π/6, F(x)= - cos 3x pri π/6<х≤ π/3, 1 za x> π/3. Nađite funkciju diferencijalne distribucije f(x), a također R(2π /9<Х< π /2). 2.3.
0 pri x≤2, f(x)= c x na 2<х≤4, 0 za x>4. 2.4.
Kontinuirana slučajna varijabla X određena je gustoćom distribucije: 0 pri x≤0, f(x)= c √x na 0<х≤1, 0 za x>1. Nađi: a) broj c; b) M(X), D(X). 2.5.
https://pandia.ru/text/78/455/images/image041_3.jpg" width="36" height="39"> na x, 0 na x. Nađite: a) F(x) i konstruirajte njegov graf; b) M(X),D(X), σ(X); c) vjerojatnost da u četiri nezavisni testovi vrijednost X će uzeti točno 2 puta vrijednost koja pripada intervalu (1;4). 2.6.
Gustoća distribucije vjerojatnosti kontinuirane slučajne varijable X dana je: f(x)= 2(x-2) na x, 0 na x. Nađite: a) F(x) i konstruirajte njegov graf; b) M(X),D(X), σ (X); c) vjerojatnost da će u tri neovisna pokušaja vrijednost X poprimiti točno 2 puta vrijednost koja pripada segmentu . 2.7.
Funkcija f(x) dana je kao: https://pandia.ru/text/78/455/images/image045_4.jpg" width="43" height="38 src=">.jpg" width="16" height="15">[-√ 3/2; √3/2]. 2.8.
Funkcija f(x) dana je kao: https://pandia.ru/text/78/455/images/image046_5.jpg" width="45" height="36 src="> .jpg" width="16" height="15">[- π /4 ; π /4]. Odredite: a) vrijednost konstante c pri kojoj će funkcija biti gustoća vjerojatnosti neke slučajne varijable X; b) funkcija raspodjele F(x). 2.9.
Slučajna varijabla X, koncentrirana na interval (3;7), određena je funkcijom distribucije F(x)= . Nađite vjerojatnost da slučajna varijabla X poprimit će vrijednost: a) manju od 5, b) ne manju od 7. 2.10.
Slučajna varijabla X, koncentrirana na interval (-1;4), dana je funkcijom raspodjele F(x)= . Nađite vjerojatnost da slučajna varijabla X poprimit će vrijednost: a) manju od 2, b) ne manju od 4. 2.11.
https://pandia.ru/text/78/455/images/image049_6.jpg" width="43" height="44 src="> .jpg" width="16" height="15">. Nađi: a) broj c; b) M(X); c) vjerojatnost P(X> M(X)). 2.12.
Slučajna varijabla određena je funkcijom diferencijalne distribucije: https://pandia.ru/text/78/455/images/image050_3.jpg" width="60" height="38 src=">.jpg" width="16 height=15" height="15"> . Nađi: a) M(X); b) vjerojatnost P(X≤M(X)) 2.13.
Rem distribucija dana je gustoćom vjerojatnosti: https://pandia.ru/text/78/455/images/image052_5.jpg" width="46" height="37"> za x ≥0. Dokažite da je f(x) doista funkcija gustoće vjerojatnosti. 2.14.
Gustoća distribucije vjerojatnosti kontinuirane slučajne varijable X dana je: DIV_ADBLOCK96"> https://pandia.ru/text/78/455/images/image055_3.jpg" width="187 height=136" height="136">(Sl. 5) 2.16.
Slučajna varijabla X distribuira se prema zakonu “ pravokutni trokut"u intervalu (0;4) (slika 5). Pronaći analitički izraz za gustoću vjerojatnosti f(x) na cijelom brojevnom pravcu. Odgovori
0 pri x≤0, f(x)= https://pandia.ru/text/78/455/images/image038_17.gif" width="14" height="86"> 0 za x≤ π/6, F(x)= 3sin 3x pri π/6<х≤ π/3,
Непрерывная случайная величина Х имеет равномерный закон распределения на некотором интервале (а;b), которому принадлежат все возможные значения Х, если плотность распределения вероятностей f(x) постоянная на этом интервале и равна 0 вне его, т. е. 0 za x≤a, f(x)= za a<х 0 za x≥b. Graf funkcije f(x) prikazan je na sl. 1 F(x)= https://pandia.ru/text/78/455/images/image077_3.jpg" width="30" height="37">, D(X)=, σ(X)=. Zadatak br. 1. Slučajna varijabla X jednoliko je raspoređena na segmentu. Pronaći: a) gustoću distribucije vjerojatnosti f(x) i nacrtajte je; b) funkciju distribucije F(x) i nacrtajte je; c) M(X),D(X), σ(X). Riješenje:
Koristeći formule o kojima smo raspravljali gore, s a=3, b=7, nalazimo: https://pandia.ru/text/78/455/images/image081_2.jpg" width="22" height="39"> na 3≤h≤7, 0 za x>7 Izgradimo njegov grafikon (Sl. 3): https://pandia.ru/text/78/455/images/image038_17.gif" width="14" height="86 src="> 0 na x≤3, F(x)= https://pandia.ru/text/78/455/images/image084_3.jpg" width="203" height="119 src=">Sl. 4 D(X) = ==https://pandia.ru/text/78/455/images/image089_1.jpg" width="37" height="43">==https://pandia.ru/text/ 78/455/images/image092_10.gif" width="14" height="49 src="> 0 na x<0, f(x)= λe-λh za x≥0. Funkcija distribucije slučajne varijable X, raspodijeljena prema eksponencijalnom zakonu, dana je formulom: DIV_ADBLOCK98"> https://pandia.ru/text/78/455/images/image095_4.jpg" width="161" height="119 src="> Sl. 6 Matematičko očekivanje, varijanca i standardna devijacija eksponencijalne distribucije jednaki su: M(X)= , D(X)=, σ (H)= Stoga su matematičko očekivanje i standardna devijacija eksponencijalne distribucije međusobno jednaki. Vjerojatnost da X padne u interval (a;b) izračunava se po formuli: Godišnje<Х Zadatak br. 2. Prosječno vrijeme rada uređaja bez kvara je 100 sati. Uz pretpostavku da vrijeme rada uređaja bez kvara ima eksponencijalni zakon raspodjele, nađite: a) gustoća distribucije vjerojatnosti; b) distribucijska funkcija; c) vjerojatnost da će vrijeme rada uređaja bez greške prijeći 120 sati. Riješenje:
Prema uvjetu, matematička distribucija M(X)=https://pandia.ru/text/78/455/images/image098_10.gif" height="43 src="> 0 na x<0, a) f(x)= 0,01e -0,01x za x≥0. b) F(x)= 0 na x<0, 1-e -0,01x pri x≥0. c) Željenu vjerojatnost nalazimo pomoću funkcije distribucije: P(X>120)=1-F(120)=1-(1- e -1,2)= e -1,2≈0,3. §
3. Zakon normalne distribucije Definicija:
Kontinuirana slučajna varijabla X ima normalno pravo raspodjele (Gaussov zakon),
ako njegova gustoća distribucije ima oblik: gdje je m=M(X), σ2=D(X), σ>0. Krivulja normalne distribucije naziva se normalna ili Gaussova krivulja
(Sl.7) Funkcija distribucije slučajne varijable X, distribuirana prema normalnom zakonu, izražava se preko Laplaceove funkcije F (x) prema formuli: gdje je Laplaceova funkcija. Komentar:
Funkcija F(x) je neparna (F(-h)=-F(h)), osim toga, za x>5 možemo pretpostaviti da je F(h) ≈1/2. Graf funkcije distribucije F(x) prikazan je na sl. 8 https://pandia.ru/text/78/455/images/image106_4.jpg" width="218" height="33"> Vjerojatnost da je apsolutna vrijednost odstupanja manja od pozitivnog broja δ izračunava se formulom: Konkretno, za m=0 vrijedi jednakost: "Pravilo tri sigme"
Ako slučajna varijabla X ima normalan zakon raspodjele s parametrima m i σ, tada je gotovo sigurno da njezina vrijednost leži u intervalu (a-3σ; a+3σ), jer https://pandia.ru/text/78/455/images/image110_2.jpg" width="157" height="57 src=">a) b) Upotrijebimo formulu: https://pandia.ru/text/78/455/images/image112_2.jpg" width="369" height="38 src="> Iz tablice vrijednosti funkcije F(h) nalazimo F(1,5)=0,4332, F(1)=0,3413. Dakle, željena vjerojatnost: P(28 Zadaci za samostalan rad
3.1.
Slučajna varijabla X jednoliko je raspoređena u intervalu (-3;5). Pronaći: b) funkcija raspodjele F(x); c) numeričke karakteristike; d) vjerojatnost P(4<х<6). 3.2.
Slučajna varijabla X jednoliko je raspoređena na segmentu. Pronaći: a) gustoća raspodjele f(x); b) funkcija raspodjele F(x); c) numeričke karakteristike; d) vjerojatnost P(3≤h≤6). 3.3.
Na autocesti postoji automatski semafor na kojem je zeleno svjetlo upaljeno 2 minute, žuto 3 sekunde, crveno 30 sekundi itd. Automobil se vozi autocestom u slučajnom trenutku. Nađite vjerojatnost da će automobil proći pored semafora bez zaustavljanja. 3.4.
Vlakovi podzemne voze redovito u intervalima od 2 minute. Putnik ulazi na peron u nasumično određeno vrijeme. Kolika je vjerojatnost da će putnik morati čekati vlak više od 50 sekundi? Nađite matematičko očekivanje slučajne varijable X - vrijeme čekanja vlaka. 3.5.
Nađite varijancu i standardnu devijaciju eksponencijalne distribucije dane funkcijom distribucije: F(x)= 0 na x<0, 1.-8x za x≥0. 3.6.
Kontinuirana slučajna varijabla X određena je gustoćom distribucije vjerojatnosti: f(x)= 0 na x<0, 0,7 e-0,7x pri x≥0. a) Navedite zakon raspodjele slučajne varijable o kojoj se radi. b) Pronađite funkciju distribucije F(X) i numeričke karakteristike slučajne varijable X. 3.7.
Slučajna varijabla X distribuira se prema eksponencijalnom zakonu određenom gustoćom distribucije vjerojatnosti: f(x)= 0 na x<0, 0,4 e-0,4 x pri x≥0. Odredite vjerojatnost da će kao rezultat testa X uzeti vrijednost iz intervala (2,5;5). 3.8.
Kontinuirana slučajna varijabla X raspoređena je prema eksponencijalnom zakonu određenom funkcijom distribucije: F(x)= 0 na x<0, 1.-0,6x pri x≥0 Odredite vjerojatnost da će, kao rezultat testa, X uzeti vrijednost iz segmenta. 3.9.
Očekivana vrijednost i standardna devijacija normalno distribuirane slučajne varijable su 8 odnosno 2. Pronađite: a) gustoća raspodjele f(x); b) vjerojatnost da će kao rezultat testa X uzeti vrijednost iz intervala (10;14). 3.10.
Slučajna varijabla X normalno je raspodijeljena s matematičkim očekivanjem od 3,5 i varijancom od 0,04. Pronaći: a) gustoća raspodjele f(x); b) vjerojatnost da će kao rezultat testa X uzeti vrijednost iz segmenta . 3.11.
Slučajna varijabla X je normalno distribuirana s M(X)=0 i D(X)=1. Koji je od događaja: |X|≤0,6 ili |X|≥0,6 vjerojatniji? 3.12.
Slučajna varijabla X raspodijeljena je normalno s M(X)=0 i D(X)=1. Iz kojeg je intervala (-0,5;-0,1) ili (1;2) veća vjerojatnost da će uzeti vrijednost tijekom jednog testa? 3.13.
Trenutna cijena po dionici može se modelirati korištenjem normalnog zakona distribucije s M(X)=10 den. jedinice i σ (X)=0,3 den. jedinice Pronaći: a) vjerojatnost da će trenutna cijena dionice biti od 9,8 den. jedinice do 10,4 dana jedinice; b) pomoću „pravila tri sigme“ pronađite granice unutar kojih će se nalaziti trenutna cijena dionice. 3.14.
Tvar se važe bez sustavnih grešaka. Slučajne pogreške vaganja podliježu normalnom zakonu sa srednjim kvadratnim omjerom σ=5g. Odredite vjerojatnost da se u četiri neovisna pokusa neće pojaviti pogreška u tri vaganja u apsolutnoj vrijednosti 3r. 3.15.
Slučajna varijabla X normalno je raspodijeljena s M(X)=12,6. Vjerojatnost da slučajna varijabla padne u interval (11,4;13,8) je 0,6826. Nađite standardnu devijaciju σ. 3.16.
Slučajna varijabla X raspodijeljena je normalno s M(X)=12 i D(X)=36. Pronađite interval u koji će slučajna varijabla X pasti kao rezultat testa s vjerojatnošću 0,9973. 3.17.
Dio proizveden automatskim strojem smatra se neispravnim ako odstupanje X njegovog kontroliranog parametra od nazivne vrijednosti prelazi modulo 2 mjerne jedinice. Pretpostavlja se da je slučajna varijabla X normalno distribuirana s M(X)=0 i σ(X)=0,7. Koliki postotak neispravnih dijelova proizvodi stroj? 3.18.
Parametar X dijela distribuira se normalno s matematičkim očekivanjem 2 jednakim nominalnoj vrijednosti i standardnom devijacijom od 0,014. Odredite vjerojatnost da odstupanje X od nominalne vrijednosti neće prijeći 1% od nominalne vrijednosti. Odgovori
https://pandia.ru/text/78/455/images/image116_9.gif" width="14" height="110 src="> b) 0 za x≤-3, F(x)= lijevo"> 3.10.
a)f(x)= , b) R(3,1≤H≤3,7) ≈0,8185. 3.11.
|x|≥0,6. 3.12.
(-0,5;-0,1). 3.13.
a) P(9,8≤H≤10,4) ≈0,6562. 3.14.
0,111. 3.15.
σ=1,2. 3.16.
(-6;30). 3.17.
0,4%. U primjenama teorije vjerojatnosti, kvantitativne karakteristike eksperimenta su od primarne važnosti. Veličina koja se može kvantitativno odrediti i koja kao rezultat pokusa može poprimiti različite vrijednosti ovisno o slučaju naziva se nasumična varijabla. Primjeri slučajnih varijabli: 1. Koliko se puta pojavljuje paran broj bodova u deset bacanja kocke. 2. Broj pogodaka mete strijelca koji ispaljuje niz hitaca. 3. Broj fragmenata eksplozivne granate. U svakom od navedenih primjera, slučajna varijabla može poprimiti samo izolirane vrijednosti, odnosno vrijednosti koje se mogu numerirati korištenjem prirodnog niza brojeva. Takva slučajna varijabla, čije su moguće vrijednosti pojedinačni izolirani brojevi, koje ova varijabla poprima s određenim vjerojatnostima, naziva se diskretna. Broj mogućih vrijednosti diskretne slučajne varijable može biti konačan ili beskonačan (prebrojiv). Zakon raspodjele Diskretna slučajna varijabla je popis njenih mogućih vrijednosti i njihovih odgovarajućih vjerojatnosti. Zakon distribucije diskretne slučajne varijable može se zadati u obliku tablice (niz distribucije vjerojatnosti), analitički i grafički (poligon distribucije vjerojatnosti). Prilikom izvođenja eksperimenta postaje nužno procijeniti vrijednost koja se proučava "u prosjeku". Ulogu prosječne vrijednosti slučajne varijable ima numerička karakteristika tzv matematičko očekivanje, koji je određen formulom Gdje x 1 , x 2
,.. , x n– vrijednosti slučajne varijable x, A str 1 ,str 2 ,
... , str n– vjerojatnosti ovih vrijednosti (imajte na umu da str 1
+
str 2
+…+
str n =
1). Primjer. Gađanje se izvodi u metu (slika 11). Pogodak u I daje tri boda, u II – dva boda, u III – jedan bod. Broj bodova postignutih u jednom hicu jednog strijelca ima zakon raspodjele oblika Za usporedbu strijelske vještine dovoljno je usporediti prosječne vrijednosti postignutih koševa, tj. matematička očekivanja M(x) I M(Y):
M(x)
=
1
0,4
+ 2
0,2
+ 3
0,4
= 2,0, M(Y)
=
1
0,2
+ 2
0,5
+ 3
0,3
= 2,1. Drugi strijelac u prosjeku daje nešto veći broj bodova, tj. dat će bolje rezultate kada se više puta pali. Zabilježimo svojstva matematičkog očekivanja: 1. Matematičko očekivanje konstantne vrijednosti jednako je samoj konstanti: M(C)
=C. 2. Matematičko očekivanje zbroja slučajnih varijabli jednako je zbroju matematičkih očekivanja članova: M =(x 1 +
x 2 +…+
x n)=
M(x 1)+
M(x 2)+…+
M(x n). 3. Matematičko očekivanje umnoška međusobno neovisnih slučajnih varijabli jednako je umnošku matematičkih očekivanja faktora M(x 1 x 2 …
x n)
=
M(x 1)M(x 2)…
M(x n). 4. Matematička negacija binomne distribucije jednaka je umnošku broja pokušaja i vjerojatnosti da se događaj dogodi u jednom pokušaju (zadatak 4.6). M(x)
= pr. Za procjenu koliko slučajna varijabla "u prosjeku" odstupa od svog matematičkog očekivanja, tj. Kako bi se karakteriziralo širenje vrijednosti slučajne varijable u teoriji vjerojatnosti koristi se koncept disperzije. Varijanca nasumična varijabla x naziva se matematičko očekivanje kvadrata odstupanja: D(x)
=
M[(x
-
M(x)) 2 ]. Disperzija je numerička karakteristika disperzije slučajne varijable. Iz definicije je jasno da što je manja disperzija slučajne varijable, to su njezine moguće vrijednosti bliže matematičkom očekivanju, odnosno da se vrijednosti slučajne varijable bolje karakteriziraju njezinim matematičkim očekivanjem . Iz definicije proizlazi da se varijanca može izračunati pomoću formule Pogodno je izračunati varijancu pomoću druge formule: D(x)
=
M(x 2)
- (M(x)) 2 .
Disperzija ima sljedeća svojstva: 1. Varijanca konstante je nula: D(C)
=
0.
2. Konstantni faktor se može izvaditi iz predznaka disperzije kvadriranjem: D(CX)
=
C 2 D(x). 3. Varijanca zbroja nezavisnih slučajnih varijabli jednaka je zbroju varijance članova: D(x 1 +
x 2 +
x 3 +…+
x n)=
D(x 1)+
D(x 2)+…+
D(x n) 4. Varijanca binomne distribucije jednaka je umnošku broja pokušaja i vjerojatnosti događanja i nepojavljivanja događaja u jednom pokušaju: D(x)
= npq. U teoriji vjerojatnosti često se koristi numerička karakteristika jednaka kvadratnom korijenu varijance slučajne varijable. Ova numerička karakteristika naziva se srednje kvadratno odstupanje i označava se simbolom Karakterizira približnu veličinu odstupanja slučajne varijable od njezine prosječne vrijednosti i ima istu dimenziju kao slučajna varijabla. 4.1.
Strijelac ispaljuje tri hica u metu. Vjerojatnost pogotka mete svakim hicem je 0,3. Konstruirajte niz distribucije za broj pogodaka. Riješenje. Broj pogodaka je diskretna slučajna varijabla x. Svaka vrijednost x n
nasumična varijabla x odgovara određenoj vjerojatnosti P n . Zakon raspodjele diskretne slučajne varijable u ovom slučaju može se odrediti blizu distribucije. U ovom problemu x uzima vrijednosti 0, 1, 2, 3. Prema Bernoullijevoj formuli Nađimo vjerojatnosti mogućih vrijednosti slučajne varijable: R 3 (0)
= (0,7) 3 =
0,343, R 3 (1)
= R 3 (2)
= R 3 (3)
= (0,3) 3 =
0,027. Raspoređivanjem vrijednosti slučajne varijable x rastućim redoslijedom dobivamo niz distribucije: x n Imajte na umu da iznos znači vjerojatnost da slučajna varijabla xće uzeti barem jednu vrijednost među mogućim, pa je stoga ovaj događaj pouzdan 4.2
.U urni se nalaze četiri kugle s brojevima od 1 do 4. Izvade se dvije kugle. Slučajna vrijednost x– zbroj brojeva kuglica. Konstruirajte niz distribucije slučajne varijable x. Riješenje. Vrijednosti slučajne varijable x su 3, 4, 5, 6, 7. Nađimo odgovarajuće vjerojatnosti. Vrijednost slučajne varijable 3 x može se prihvatiti samo u slučaju kada jedna od odabranih kuglica ima broj 1, a druga 2. Broj mogućih ishoda testa jednak je broju kombinacija četiri (broj mogućih parova kuglica) od dvije. Korištenjem klasične formule vjerojatnosti dobivamo Također, R(x= 4) =R(x= 6) =R(x= 7) = 1/6. Zbroj 5 može se pojaviti u dva slučaja: 1 + 4 i 2 + 3, dakle x ima oblik: Pronađite funkciju distribucije F(x) nasumična varijabla x i zacrtajte ga. Izračunajte za x njegovo matematičko očekivanje i varijancu. Riješenje. Zakon raspodjele slučajne varijable može se specificirati funkcijom raspodjele F(x)
= P(x
x).
Funkcija distribucije F(x) je neopadajuća, lijevo kontinuirana funkcija definirana na cijelom brojevnom pravcu, dok F
(-
)=
0,F
(+
)=
1. Za diskretnu slučajnu varijablu ova se funkcija izražava formulom Stoga u ovom slučaju Grafik funkcije distribucije F(x) je stepenasta linija (Sl. 12) F(x) Očekivana vrijednostM(x) je ponderirani aritmetički prosjek vrijednosti x 1 , X 2 ,……X n nasumična varijabla x s vagama ρ
1,
ρ
2, ……
, ρ
n
a naziva se srednja vrijednost slučajne varijable x. Prema formuli M(x)= x 1
ρ
1 + x 2
ρ
2 +……+ x n
ρ
n M(x) = 3·0,14+5·0,2+7·0,49+11·0,17 = 6,72. Disperzija karakterizira stupanj disperzije vrijednosti slučajne varijable od njezine prosječne vrijednosti i označava se D(x): D(x)=M[(HM(x)) 2 ]= M(x 2)
–[M(x)] 2 . Za diskretnu slučajnu varijablu varijanca ima oblik ili se može izračunati pomoću formule Zamjenom numeričkih podataka problema u formulu dobivamo: M(x 2)
=
3 2
∙ 0,14+5 2
∙ 0,2+7 2
∙ 0,49+11 2
∙ 0,17 = 50,84 D(x)
= 50,84-6,72 2
= 5,6816. 4.4.
Dvije se kockice bacaju dvaput u isto vrijeme. Napišite binomni zakon raspodjele diskretne slučajne varijable x- broj pojavljivanja parnog ukupnog broja bodova na dvije kocke. Riješenje. Uvedimo slučajni događaj A= (dvije kocke jednim bacanjem dale su ukupni paran broj bodova). Koristeći se klasičnom definicijom vjerojatnosti nalazimo R(A)=
Gdje n
- broj mogućih ishoda testa nalazi se prema pravilu množenje: n
= 6∙6 =36, m
-
broj ljudi koji favoriziraju događaj A ishodi – jednaki m= 3∙6=18. Dakle, vjerojatnost uspjeha u jednom pokušaju je ρ
= P(A)=
1/2.
Problem se rješava pomoću Bernoullijeve sheme testa. Jedan izazov ovdje bit će bacanje dvije kockice jednom. Broj takvih testova n
= 2. Slučajna varijabla x uzima vrijednosti 0, 1, 2 s vjerojatnostima R 2 (0)
= Tražena binomna distribucija slučajne varijable x može se predstaviti kao serija distribucije: x n ρ
n 4.5
. U seriji od šest dijelova nalaze se četiri standardna. Nasumično su odabrana tri dijela. Konstruirajte distribuciju vjerojatnosti diskretne slučajne varijable x– broj standardnih dijelova među odabranima i pronađite njegovo matematičko očekivanje. Riješenje. Vrijednosti slučajne varijable x su brojevi 0,1,2,3. Jasno je da R(x=0)=0, jer postoje samo dva nestandardna dijela. R(x=1) = R(X= 2) = R(x=3) = Zakon raspodjele slučajne varijable x Predstavimo ga u obliku serije distribucije: x n ρ
n Očekivana vrijednost M(x)=1
∙ 1/5+2 ∙ 3/5+3 ∙ 1/5=2. 4.6
. Dokažite da je matematičko očekivanje diskretne slučajne varijable x- broj pojavljivanja događaja A V n neovisna ispitivanja, u svakom od kojih je vjerojatnost događanja događaja jednaka ρ
– jednaka umnošku broja pokušaja s vjerojatnošću pojave događaja u jednom pokušaju, odnosno dokazati da je matematičko očekivanje binomne distribucije M(x)
=n .
ρ
, i disperzija D(x)
=n.p.
. Riješenje. Slučajna vrijednost x može poprimiti vrijednosti 0, 1, 2..., n. Vjerojatnost R(x= k) nalazi se pomoću Bernoullijeve formule: R(x=k)= R n(k)= Niz distribucije slučajne varijable x ima oblik: x n ρ
n q n Gdje q=
1-
ρ
. Za matematičko očekivanje imamo izraz: M(x)= U slučaju jednog testa, odnosno sa n= 1 za slučajnu varijablu x 1 – broj pojavljivanja događaja A- serija distribucije ima oblik: x n ρ
n M(x 1)=
0∙q +
1
∙ str
=
str D(x 1)
=
str
–
str 2
=
str(1-
str)
=
pq. Ako x k – broj pojavljivanja događaja A u kojem testu, dakle R(x Do)=
ρ
I X=X 1 +X 2 +….+X n . Odavde dobivamo M(x)=M(x 1
)+M(x 2)+
… +M(x n)=
nρ,
D(x)=D(x 1)+D(x 2)+
...
+D(x n)=npq. 4.7.
Odjel kontrole kvalitete provjerava standardnost proizvoda. Vjerojatnost da je proizvod standardan je 0,9. Svaka serija sadrži 5 proizvoda. Nađite matematičko očekivanje diskretne slučajne varijable x- broj serija od kojih će svaka sadržavati 4 standardna proizvoda - ako je pregledu 50 serija. Riješenje. Vjerojatnost da će u svakoj nasumično odabranoj seriji biti 4 standardna proizvoda je konstantna; označimo to sa ρ
.Zatim matematičko očekivanje slučajne varijable x jednaki M(x)=
50∙ρ.
Nađimo vjerojatnost ρ
prema Bernoullijevoj formuli: ρ=P 5 (4)= M(x)=
50∙0,32=16. 4.8
. Bacaju se tri kocke. Nađite matematičko očekivanje zbroja ispuštenih bodova. Riješenje. Možete pronaći distribuciju slučajne varijable x- zbroj izgubljenih bodova i zatim njegovo matematičko očekivanje. Međutim, ovaj put je previše glomazan. Lakše je koristiti drugu tehniku, koja predstavlja slučajnu varijablu x, čije matematičko očekivanje treba izračunati, u obliku zbroja više jednostavnijih slučajnih varijabli, čije je matematičko očekivanje lakše izračunati. Ako je slučajna varijabla x ja je broj otkotrljanih bodova ja– th kosti ( ja= 1, 2, 3), zatim zbroj bodova xće se izraziti u obliku X = X 1 + X 2 + X 3 . Za izračunavanje matematičkog očekivanja izvorne slučajne varijable, sve što preostaje jest koristiti svojstvo matematičkog očekivanja M(x 1
+ X 2 + X 3
)= M(x 1
)+ M(x 2)+ M(x 3
). Očito je da R(x ja = K)=
1/6, TO=
1, 2, 3, 4, 5, 6,
ja=
1,
2, 3. Dakle, matematičko očekivanje slučajne varijable x ja izgleda kao M(x ja)
=
1/6∙1
+ 1/6∙2
+1/6∙3
+ 1/6∙4
+ 1/6∙5
+ 1/6∙6
= 7/2, M(x)
=
3∙7/2 = 10,5.
4.9.
Odredite matematičko očekivanje broja uređaja koji nisu uspjeli tijekom testiranja ako: a) vjerojatnost kvara za sve uređaje je ista R, a broj uređaja koji se testiraju jednak je n; b) vjerojatnost kvara za ja
–
uređaja jednako je str ja
,
ja=
1,
2, … , n. Riješenje. Neka je slučajna varijabla x je broj neispravnih uređaja, dakle X = X 1 + X 2 + … + X n ,
x ja
=
Jasno je da R(x ja =
1)=
R ja ,
R(x ja =
0)=
1–
R ja ,i= 1,
2,
…
,n. M(x ja)=
1∙R ja +
0∙(1-R ja)=P ja , M(x)=M(x 1)+M(x 2)+ … +M(x n)=P 1 +P 2 + … + P n .
U slučaju "a" vjerojatnost kvara uređaja je ista, tj R ja =str,i= 1,
2, …
,n. M(x)=
n.p.. Ovaj odgovor možemo dobiti odmah ako primijetimo da je slučajna varijabla x ima binomnu distribuciju s parametrima ( n,
str).
4.10.
Dvije kocke bacaju se istovremeno dva puta. Napišite binomni zakon raspodjele diskretne slučajne varijable X - broj bacanja parnog broja bodova na dvije kocke. Riješenje. Neka A=(bacanje parnog broja na prvoj kockici), B =(bacanje parnog broja na drugu kockicu). Dobivanje parnog broja na obje kocke u jednom bacanju izražava se umnoškom AB. Zatim R
(AB)
= R(A)∙R(U)
=
Rezultat drugog bacanja dviju kockica ne ovisi o prvom, pa Bernoullijeva formula vrijedi kada n
=
2,p = 1/4,
q
=
1– p = 3/4.
Slučajna vrijednost x može poprimiti vrijednosti 0, 1, 2 ,
čija se vjerojatnost može pronaći pomoću Bernoullijeve formule: R(X= 0)= P 2
(0)
=
q
2
= 9/16, R(X= 1)= P 2
(1)= C R(X= 2)= P 2
(2)= C Niz distribucije slučajne varijable X: 4.11.
Uređaj se sastoji od velikog broja neovisno aktivnih elemenata s istom vrlo malom vjerojatnošću kvara svakog elementa tijekom vremena t. Pronađite prosječan broj odbijanja tijekom vremena t elemenata, ako je vjerojatnost da barem jedan element zakaže tijekom tog vremena 0,98. Riješenje.
Broj ljudi koji su odbili tijekom vremena t elementi – slučajna varijabla x, koji je raspodijeljen prema Poissonovom zakonu, budući da je broj elemenata velik, elementi rade neovisno i vjerojatnost kvara svakog elementa je mala. Prosječan broj pojavljivanja događaja u n testovi jednaki M(x)
=
n.p..
Budući da je vjerojatnost neuspjeha DO elementi iz n izražen formulom R n
(DO)
gdje je
=
n.p., zatim vjerojatnost da niti jedan element neće otkazati tijekom vremena t
dobivamo na K = 0: R n
(0)= e - . Stoga je vjerojatnost suprotnog događaja u vremenu t
barem jedan element ne uspije – jednako 1 - e -
. Prema uvjetima zadatka ta je vjerojatnost 0,98. Iz jednadžbe 1
- e -
= 0,98, e -
= 1 – 0,98 =
0,02, odavde
=
-ln
0,02
4. Dakle, na vrijeme t rada uređaja, u prosjeku će 4 elementa otkazati. 4.12
. Kocka se baca sve dok se ne pojavi “dvojka”. Nađite prosječan broj bacanja. Riješenje. Uvedimo slučajnu varijablu x– broj testova koji se moraju obaviti dok se ne dogodi događaj koji nas zanima. Vjerojatnost da x= 1 jednaka je vjerojatnosti da se tijekom jednog bacanja kocke pojavi “dvojka”, tj. R(X= 1)
= 1/6. Događaj x= 2 znači da se na prvom testu "dvojka" nije pojavila, ali na drugom jest. Vjerojatnost događaja x= 2 nalazi se pravilom množenja vjerojatnosti neovisnih događaja: R(X= 2)
= (5/6)∙(1/6) Također, R(X= 3)
= (5/6) 2 ∙1/6, R(X= 4)
= (5/6) 2 ∙1/6 itd. Dobivamo niz distribucija vjerojatnosti: (5/6) Do
∙1/6 Prosječan broj bacanja (pokusa) je matematičko očekivanje M(x)
=
1∙1/6 +
2∙5/6∙1/6 + 3∙(5/6) 2 ∙1/6
+ … + DO
(5/6) DO -1 ∙1/6
+ … = 1/6∙(1+2∙5/6 +3∙(5/6) 2
+ … + DO
(5/6) DO -1
+ …) Nađimo zbroj niza: Stoga, M(x)
=
(1/6) (1/ (1 –
5/6) 2
= 6. Dakle, trebate u prosjeku napraviti 6 bacanja kocke dok se ne pojavi “dvojka”. 4.13.
Nezavisni testovi se provode s istom vjerojatnošću pojavljivanja događaja A u svakom testu. Odredite vjerojatnost događanja događaja A, ako je varijanca broja pojavljivanja događaja u tri neovisna pokusa 0,63 .
Riješenje. Broj pojavljivanja događaja u tri pokusa je slučajna varijabla x, raspodijeljen prema binomnom zakonu. Varijanca broja pojavljivanja događaja u neovisnim pokusima (s istom vjerojatnošću pojavljivanja događaja u svakom pokusu) jednaka je umnošku broja pokusa s vjerojatnostima pojavljivanja i nepojavljivanja događaja (problem 4.6) D(x)
=
npq.
Po stanju n
=
3,
D(x)
=
0,63, tako da možete R pronaći iz jednadžbe 0,63
= 3∙R(1-R), koji ima dva rješenja R 1
=
0,7 i R 2
=
0,3. Diskretna
zove se slučajna varijabla koja može poprimiti pojedinačne, izolirane vrijednosti s određenim vjerojatnostima. PRIMJER 1. Broj pojavljivanja grba u tri bacanja novčića. Moguće vrijednosti: 0, 1, 2, 3, njihove su vjerojatnosti jednake redom: P(0) = ; R(1) = ; R(2) = ; R(3) = .
PRIMJER 2. Broj pokvarenih elemenata u uređaju koji se sastoji od pet elemenata. Moguće vrijednosti: 0, 1, 2, 3, 4, 5; njihove vjerojatnosti ovise o pouzdanosti svakog elementa. Diskretna slučajna varijabla x može biti dana nizom distribucije ili funkcijom distribucije (integralni zakon distribucije). Blizu distribucije
je skup svih mogućih vrijednosti xja i njihove odgovarajuće vjerojatnosti Ri = P(X = xja),
može se odrediti kao tablica: x i x n p i r n Istodobno, vjerojatnosti Rja zadovoljiti uvjet Rja= 1 jer gdje je broj mogućih vrijednosti n može biti konačan ili beskonačan. Grafički prikaz serija distribucije koji se naziva poligon distribucije
. Da bismo ga konstruirali, moguće vrijednosti slučajne varijable ( xja) iscrtavaju se duž x-osi, a vjerojatnosti Rja- duž ordinatne osi; bodova Aja s koordinatama ( xi,rja) povezani su isprekidanim linijama. Funkcija distribucije
nasumična varijabla
x nazvana funkcija F(x),
čija vrijednost u točki x jednaka je vjerojatnosti da slučajna varijabla x bit će manji od ove vrijednosti x, to je F(x) = P(X< х). Funkcija F(x)
Za diskretna slučajna varijabla izračunati po formuli F(X) =
Rja ,
(1.10.1) gdje se zbrajanje provodi po svim vrijednostima ja, za koji xja<
х.
PRIMJER 3. Iz serije od 100 proizvoda, od kojih je 10 neispravno, nasumično se odabire pet proizvoda radi provjere njihove kvalitete. Konstruirajte niz distribucija slučajnog broja x neispravne proizvode sadržane u uzorku. Riješenje.
Budući da u uzorku broj neispravnih proizvoda može biti bilo koji cijeli broj u rasponu od 0 do uključivo 5, tada moguće vrijednosti xja nasumična varijabla x su jednaki: x 1 = 0, x 2 = 1, x 3 = 2, x 4 = 3, x 5 = 4, x 6 = 5. Vjerojatnost R(X = k)
da uzorak točno sadrži
k(k =
0, 1, 2, 3, 4, 5) neispravni proizvodi, jednako P (X = k) = . Kao rezultat izračuna pomoću ove formule s točnošću od 0,001, dobivamo: R 1 = P(X = 0) @ 0,583;R 2 = P(X = 1) @ 0,340;R 3 = P(X = 2) @ 0,070; R 4 = P(X = 3) @ 0,007;R 5 = P(x= 4) @ 0;R 6 = P(X = 5) @ 0.
Korištenje jednakosti za provjeru Rk=1, uvjeravamo se da su izračuni i zaokruživanje ispravno obavljeni (vidi tablicu). x i p i PRIMJER 4. Zadan niz distribucije slučajne varijable x : x i p i Pronađite funkciju distribucije vjerojatnosti
F(x) ove slučajne varijable i konstruirajte je. Riješenje.
Ako x Onda 10 funti
F(x)= P(x<x) = 0; ako 10<x Onda 20 funti
F(x)= P(x<x) = 0,2 ;
ako 20<x Onda 30 funti
F(x)= P(x<x) = 0,2 + 0,3 = 0,5 ;
ako 30<x Onda 40 funti
F(x)= P(x<x) = 0,2 + 0,3 + 0,35 = 0,85 ; ako 40<x Onda 50 funti
F(x)= P(x<x) = 0,2 + 0,3 + 0,35 + 0,1=0,95 ; Ako x> 50, dakle
F(x)= P(x<x) = 0,2 + 0,3 + 0,35 + 0,1 + 0,05 = 1.

 1.2.
p4=0,1; 0 pri x≤-1,
1.2.
p4=0,1; 0 pri x≤-1,

![]()
 https://pandia.ru/text/78/455/images/image038_17.gif" width="14" height="86"> 0 za x≤a,
https://pandia.ru/text/78/455/images/image038_17.gif" width="14" height="86"> 0 za x≤a, ,
, Normalna krivulja je simetrična u odnosu na ravnu liniju x=m, ima maksimum pri x=a, jednak .
Normalna krivulja je simetrična u odnosu na ravnu liniju x=m, ima maksimum pri x=a, jednak .
![]() ,
,![]()
![]()


 .
.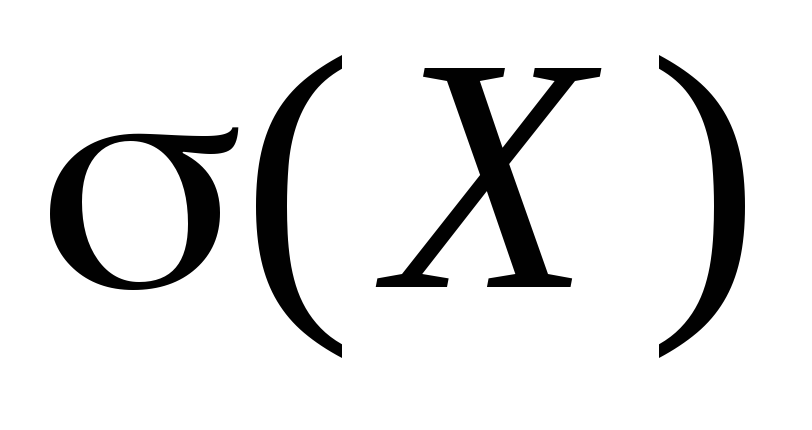 .
. ,
, 0,3(0,7) 2
= 0,441,
0,3(0,7) 2
= 0,441, (0,3) 2 0,7
= 0,189,
(0,3) 2 0,7
= 0,189,

 .
.
 .
. .
.

 ,
,
 ,R 2 (1)
=
,R 2 (1)
= ∙
∙ ,R 2 (2)
=
,R 2 (2)
=
 =1/5,
=1/5, = 3/5,
= 3/5, = 1/5.
= 1/5.
 ρ
Do
(1-ρ
) n- Do
ρ
Do
(1-ρ
) n- Do
 ρq n- 1
ρq n- 1
 ρq n- 2
ρq n- 2
 ρ
n
ρ
n ρq n -
1
+2
ρq n -
1
+2
 ρ
2
q n -
2
+…+.n
ρ
2
q n -
2
+…+.n
 ρ
n
ρ
n
 = 0,94∙0,1=0,32.
= 0,94∙0,1=0,32.
 .
. ,R∙q
=
6/16,
,R∙q
=
6/16, ,
R 2
=
1/16.
,
R 2
=
1/16.
 ,
,
 DOg
DO -1
= (
DOg
DO -1
= ( g DO)
g
g DO)
g
 .
.

